题目内容
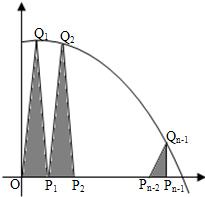 如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1,△Q2P1P2,…,△Qn-1Pn-2Pn-1.当n→∞时,这些三角形的面积之和的极限为
如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1,△Q2P1P2,…,△Qn-1Pn-2Pn-1.当n→∞时,这些三角形的面积之和的极限为分析:由题意知
(S1+S2+…+Sn-1)=
[(n-1)-
],由此能够推导出这些三角形的面积之和的极限.
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2n |
| 12+ 22+…+(n-1)2 |
| n2 |
解答:解:p1(
,0),p2(
,0),…,pn-1(
,0);Q1(
,1-(
)2),Q2(
,1-(
)2),…,Qn-1(
,1-(
)2),记△QnPn-1Pn的面积为Sn,则S1=
-
-[1-(
)2],S2=
-
-[1-(
)2],…,Sn-1=
-
-[1-(
)2];
(S1+S2+…+Sn-1)=
[(n-1)-
]=
-
=
-
=
.
答案:
.
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 2 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n-1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| n-1 |
| n |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2n |
| 12+ 22+…+(n-1)2 |
| n2 |
| 1 |
| 2 |
| lim |
| n→∞ |
| (n-1)(n-2)(2n-3) |
| 12n3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
答案:
| 1 |
| 3 |
点评:本题考查极限的求法,解题时要注意观察分析能力和归纳总结能力的培养.

练习册系列答案
相关题目
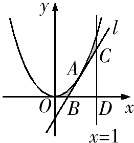 如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D.
如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D. 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.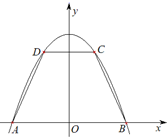 (2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
(2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S. 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.