Question

【题目】已知关于的方程有实数根b.

（1）求实数的值.

（2）若复数满足. 求z为何值时，|z|有最小值，并求出|z|的最小值.

Answer 1

【答案】(1);(2) 当z=1﹣i时,|z|有最小值且|z|min=．

【解析】试题分析：（1）复数方程有实根，方程化简为（a、b∈R），利用复数相等，即，解方程组即可．

（2）先把a、b代入方程，同时设复数，化简方程，根据表达式的几何意义，方程表示圆，

再数形结合，求出z，得到|z|．

试题解析：解：（1）∵是方程的实根

∴（2分）

∴解得（4分）

（2）设，其对应点为

由得： 即

∴点的轨迹是以O1（－1，1）为圆心， 为半径的圆，如图所示（8分）

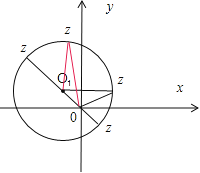
当点在OO1的连线上时， 有或∵

∴当时， 有最小值，且（10分）