题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(1)求 的大小;
的大小;
(2)若 ,求
,求 的取值范围.
的取值范围.
(1)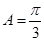 ;(2)
;(2)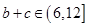 .
.
解析试题分析:(1)由条件结合正弦定理,构建关于 的方程,从而解出
的方程,从而解出 的值.(2)求
的值.(2)求 的取值范围,通过正弦定理转化为角
的取值范围,通过正弦定理转化为角 或角
或角 的三角函数,运用三角函数的知识解决问题,注意角
的三角函数,运用三角函数的知识解决问题,注意角 的范围.在三角函数中求式子的取值范围,通常是运用正、余弦定理转化为某个角的三角函数来求范围,很少转化为某条边的代数函数来求范围的.
的范围.在三角函数中求式子的取值范围,通常是运用正、余弦定理转化为某个角的三角函数来求范围,很少转化为某条边的代数函数来求范围的.
试题解析:(1)由已知条件结合正弦定理有: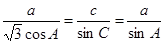 ,从而有:
,从而有: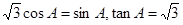 ,
,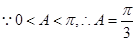 .
.
(2)由正弦定理得: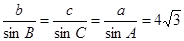 ,
,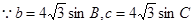 ,
,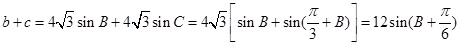
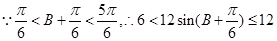 ,即:
,即: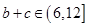 .
.
考点:1.解三角形;2.三角函数图象与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 点D、E分别为AC、BC边的中点,且BD=
点D、E分别为AC、BC边的中点,且BD= ,
, 的内角
的内角 所对边的长分别是
所对边的长分别是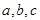 ,且
,且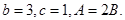
 的值; (Ⅱ)求
的值; (Ⅱ)求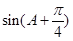 的值.
的值. 中,角
中,角 对的边分别为
对的边分别为 ,且
,且 .
. 的值;
的值; ,求
,求 .
.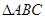 中,
中,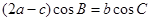
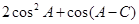 的取值范围.
的取值范围. 中,角
中,角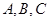 所对的边分别为
所对的边分别为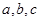 ,已知
,已知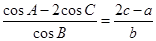 .
. 的值;
的值;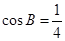 ,
, ,求△
,求△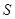 .
. ,
, ,求三角形ABC的面积.
,求三角形ABC的面积. ,
, ,则角A= .
,则角A= .  中,
中, ,则
,则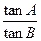 = 。
= 。