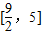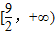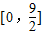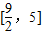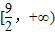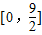题目内容
已知实数a≥0,b≥0且a+b=1,则(a+1)2+(b+1)2的取值范围为A.[
 ,5]B.[
,5]B.[ ,+∞) C.[0,
,+∞) C.[0, ]D.[0,5].
]D.[0,5].
【答案】分析:由题意(a+1)2+(b+1)2的取值范围,就是线段上的点到(-1,-1)的距离的平方范围.
解答:解:(a+1)2+(b+1)2的取值范围,转化为实数a≥0,b≥0,且a+b=1的线段上的点到(-1,-1)的距离的平方范围,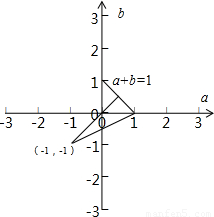
由图象可知,(-1,-1)到( ,
, )距离最小,即(
)距离最小,即( +1)2+(
+1)2+( +1)2=
+1)2=
(-1,-1)到(1,0)距离最大,即(1+1)2+(0+1)2=5
所以(a+1)2+(b+1)2的取值范围:[ ,5].
,5].
故选A.
点评:本题考查两点的距离公式的应用,简单的线性规划,考查转化思想,计算能力.
解答:解:(a+1)2+(b+1)2的取值范围,转化为实数a≥0,b≥0,且a+b=1的线段上的点到(-1,-1)的距离的平方范围,
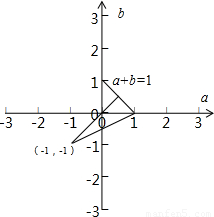
由图象可知,(-1,-1)到(
 ,
, )距离最小,即(
)距离最小,即( +1)2+(
+1)2+( +1)2=
+1)2=
(-1,-1)到(1,0)距离最大,即(1+1)2+(0+1)2=5
所以(a+1)2+(b+1)2的取值范围:[
 ,5].
,5].故选A.
点评:本题考查两点的距离公式的应用,简单的线性规划,考查转化思想,计算能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目