题目内容
5.已知数列{an}的前n项和为Sn,且an=Sn•Sn-1(n≥2),a1=$\frac{2}{9}$,则an=$\left\{\begin{array}{l}{\frac{2}{9},}&{n=1}\\{\frac{4}{(11-2n)(13-2n)},}&{n≥2}\end{array}\right.$.分析 利用an=Sn-Sn-1并对等式Sn-Sn-1=Sn•Sn-1(n≥2)两边同时取倒数可知数列{$\frac{1}{{S}_{n}}$}是以$\frac{9}{2}$为首项、-1为公差的等差数列,进而计算可得结论.
解答 解:∵an=Sn-Sn-1=Sn•Sn-1(n≥2),
∴$\frac{{S}_{n}-{S}_{n-1}}{{S}_{n}{•S}_{n-1}}$=$\frac{{S}_{n}•{S}_{n-1}}{{S}_{n}•{S}_{n-1}}$,即$\frac{1}{{S}_{n-1}}$-$\frac{1}{{S}_{n}}$=1,
∴$\frac{1}{{S}_{n}}$=$\frac{1}{{S}_{n-1}}$-1,
又∵$\frac{1}{{a}_{1}}$=$\frac{9}{2}$,
∴数列{$\frac{1}{{S}_{n}}$}是以$\frac{9}{2}$为首项、-1为公差的等差数列,
∴$\frac{1}{{S}_{n}}$=$\frac{9}{2}$-(n-1)=$\frac{11}{2}$-n=$\frac{-2n+11}{2}$,
∴Sn=$\frac{2}{-2n+11}$,
∴an+1=Sn+1-Sn
=$\frac{2}{-2(n+1)+11}$-$\frac{2}{-2n+11}$
=$\frac{4}{(-2n+9)(-2n+11)}$,
又∵a1=$\frac{2}{9}$不满足上式,
∴an=$\left\{\begin{array}{l}{\frac{2}{9},}&{n=1}\\{\frac{4}{(11-2n)(13-2n)},}&{n≥2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{\frac{2}{9},}&{n=1}\\{\frac{4}{(11-2n)(13-2n)},}&{n≥2}\end{array}\right.$.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
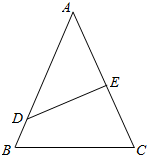 某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.
某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.