题目内容
下列说法中:
①若函数f(x)=ax2+(2a+b)x+2(x∈[2a﹣1,a+4])是偶函数,则实数b=2;
②f(x)表示﹣2x+2与﹣2x2+4x+2中的较小者,则函数f(x)的最大值为1;
③已知函数f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),则f(x)是奇函数;
④设lg2=a,lg3=b那么可以得到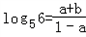 ;
;
⑤函数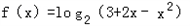 的值域是(0,2),
的值域是(0,2),
其中正确说法的序号是( )(注:把你认为是正确的序号都填上).
①若函数f(x)=ax2+(2a+b)x+2(x∈[2a﹣1,a+4])是偶函数,则实数b=2;
②f(x)表示﹣2x+2与﹣2x2+4x+2中的较小者,则函数f(x)的最大值为1;
③已知函数f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),则f(x)是奇函数;
④设lg2=a,lg3=b那么可以得到
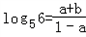 ;
;⑤函数
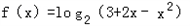 的值域是(0,2),
的值域是(0,2),其中正确说法的序号是( )(注:把你认为是正确的序号都填上).
①③④

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;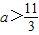 ;
; 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点; ;
;