题目内容
下列说法中:①函数
 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;②若定义在R上的函数f(x)满足f(x+2)=-f(x-1),则6为函数f(x)的周期;
③若对于任意x∈(1,3),不等式x2-ax+2<0恒成立,则
 ;
;④定义:“若函数f(x)对于任意x∈R,都存在正常数M,使|f(x)|≤M|x|恒成立,则称函数f(x)为有界泛函.”由该定义可知,函数f(x)=x2+1为有界泛函.
则其中正确的个数为 .
【答案】分析:联立两个函数的解析式,构造方程组,方程组解的个数即为函数图象交点个数,由此可判断①的真假,根据周期函数的定义可判断②的真假,根据二次函数的性质,我们可构造关于a的不等式组,解不等式组,即可求出a的取值范围,进而判断③的真假,根据二次函数的性质结合有界泛函的定义,可以判断④的真假,进而得到答案.
解答:解:联立两个函数的解析式, ,易得该方程组无解,则①函数
,易得该方程组无解,则①函数 与g(x)=x的图象没有公共点,正确;
与g(x)=x的图象没有公共点,正确;
定义在R上的函数f(x)满足f(x+2)=-f(x-1),则f(x+3)=-f(x),f(x+6)=-f(x+3)=f(x),故f(x)的周期为6,故②正确;
若对于任意x∈(1,3),不等式x2-ax+2<0恒成立,令f(x)=x2-ax+2,则f(1)<0且f(3)<0,解得 ,故③正确;
,故③正确;
当x>0时,不存在正常数M使|x2+1|=x2+1≤M|x|=Mx恒成立,故④错误;
故答案为:3
点评:本题考查的知识点是命题的真假判断与应用,函数的周期性,函数恒成立问题,熟练掌握函数的性质及不等式与对应函数之间的辩证关系是解答本题的关键.
解答:解:联立两个函数的解析式,
 ,易得该方程组无解,则①函数
,易得该方程组无解,则①函数 与g(x)=x的图象没有公共点,正确;
与g(x)=x的图象没有公共点,正确;定义在R上的函数f(x)满足f(x+2)=-f(x-1),则f(x+3)=-f(x),f(x+6)=-f(x+3)=f(x),故f(x)的周期为6,故②正确;
若对于任意x∈(1,3),不等式x2-ax+2<0恒成立,令f(x)=x2-ax+2,则f(1)<0且f(3)<0,解得
 ,故③正确;
,故③正确;当x>0时,不存在正常数M使|x2+1|=x2+1≤M|x|=Mx恒成立,故④错误;
故答案为:3
点评:本题考查的知识点是命题的真假判断与应用,函数的周期性,函数恒成立问题,熟练掌握函数的性质及不等式与对应函数之间的辩证关系是解答本题的关键.

练习册系列答案
相关题目
 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;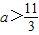 ;
;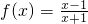 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;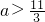 ;
;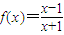 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;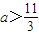 ;
;