题目内容
已知定义在R上的二次函数R(x)=ax2+bx+c满足2R(-x)-2R(x)=0,且R(x)的最小值为0,函数h(x)=lnx,又函数f(x)=h(x)-R(x).(I)求f(x)的单调区间;
(II)当a≤
 时,若x∈[1,3],求f(x)的最小值;
时,若x∈[1,3],求f(x)的最小值;(III)若二次函数R(x)图象过(4,2)点,对于给定的函数f(x)图象上的点A(x1,y1),当
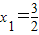 时,探求函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.(参考数据:e=2.71828…)
时,探求函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.(参考数据:e=2.71828…)
【答案】分析:(I)由2R(-x)-2R(x)=0,知R(-x)=R(x),故R(x)=ax2+c.所以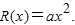 令f′(x)=0,得
令f′(x)=0,得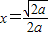 .由此能求出f(x)的单调区间.
.由此能求出f(x)的单调区间.
(II)由当0<a≤ 时,
时, ≥1,知x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.由此能求出f(x)的最小值.
≥1,知x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.由此能求出f(x)的最小值.
(III)若二次函数R(x)=ax2图象过(4,2)点,则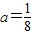 ,所以
,所以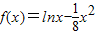 .由此能导出函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.
.由此能导出函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.
解答:解:(I)∵定义在R上的二次函数R(x)=ax2+bx+c满足2R(-x)-2R(x)=0,
∴2R(-x)-2R(x)=0,
∴2R(-x)=2R(x),即R(-x)=R(x),
∵R(x)=ax2+bx+c,∴b=0,∴R(x)=ax2+c.
∵R(x)=ax2+c的最小值为0,∴a>0,c=0,故R(x)=ax2,
∵R(x)=ax2,h(x)=lnx,f(x)=h(x)-R(x),
∴f(x)=lnx-ax2,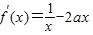 ,
,
令f′(x)=0,解得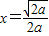 .
.
当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是(0,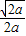 ),
),
f(x)的单调递减区间是(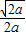 ,+∞).
,+∞).
(II)∵当0<a≤ 时,
时,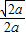 ≥1,
≥1,
∴x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.
又f(1)=-a,f(3)=1n3-9a,
f(1)-f(3)=-a-(ln3-9a)=8a-1n3.
∴当0<a≤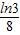 时,f(1)≤f(3),f(x)的最小值-a;
时,f(1)≤f(3),f(x)的最小值-a;
当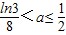 时,f(1)>f(3),f(x)的最小值ln3-9a.
时,f(1)>f(3),f(x)的最小值ln3-9a.
(III)证明:若二次函数R(x)=ax2图象过(4,2)点,则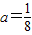 ,
,
所以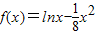 .
.
令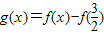 .
.
由(I)知f(x)在(0,2)内单调递增,
故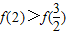 ,即g(2)>0.
,即g(2)>0.
取 ,则
,则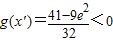 .
.
所以存在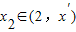 ,使g(x2)=0,
,使g(x2)=0,
故存在x2∈(2,+∞),使 .
.
所以函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.
点评:本题考查求f(x)的单调区间,求f(x)的最小值,探索函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
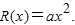 令f′(x)=0,得
令f′(x)=0,得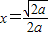 .由此能求出f(x)的单调区间.
.由此能求出f(x)的单调区间.(II)由当0<a≤
 时,
时, ≥1,知x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.由此能求出f(x)的最小值.
≥1,知x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.由此能求出f(x)的最小值.(III)若二次函数R(x)=ax2图象过(4,2)点,则
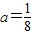 ,所以
,所以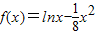 .由此能导出函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.
.由此能导出函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.解答:解:(I)∵定义在R上的二次函数R(x)=ax2+bx+c满足2R(-x)-2R(x)=0,
∴2R(-x)-2R(x)=0,
∴2R(-x)=2R(x),即R(-x)=R(x),
∵R(x)=ax2+bx+c,∴b=0,∴R(x)=ax2+c.
∵R(x)=ax2+c的最小值为0,∴a>0,c=0,故R(x)=ax2,
∵R(x)=ax2,h(x)=lnx,f(x)=h(x)-R(x),
∴f(x)=lnx-ax2,
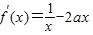 ,
,令f′(x)=0,解得
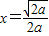 .
.当x变化时,f'(x),f(x)的变化情况如下表:
| x | (0,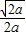 ) ) | 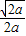 | (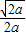 ,+∞) ,+∞) |
| f'(x) | + | - | |
| f(x) | ↑ | 极大值 | ↓ |
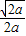 ),
),f(x)的单调递减区间是(
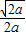 ,+∞).
,+∞).(II)∵当0<a≤
 时,
时,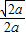 ≥1,
≥1,∴x∈[1,3]时,f(x)的最小值为f(1)与f(3)中的较小者.
又f(1)=-a,f(3)=1n3-9a,
f(1)-f(3)=-a-(ln3-9a)=8a-1n3.
∴当0<a≤
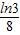 时,f(1)≤f(3),f(x)的最小值-a;
时,f(1)≤f(3),f(x)的最小值-a;当
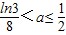 时,f(1)>f(3),f(x)的最小值ln3-9a.
时,f(1)>f(3),f(x)的最小值ln3-9a.(III)证明:若二次函数R(x)=ax2图象过(4,2)点,则
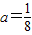 ,
,所以
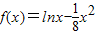 .
.令
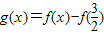 .
.由(I)知f(x)在(0,2)内单调递增,
故
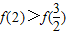 ,即g(2)>0.
,即g(2)>0.取
 ,则
,则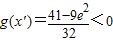 .
.所以存在
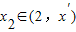 ,使g(x2)=0,
,使g(x2)=0,故存在x2∈(2,+∞),使
 .
.所以函数f(x)图象上存在点B(x2,y2)(x2>2),使A、B连线平行于x轴.
点评:本题考查求f(x)的单调区间,求f(x)的最小值,探索函数f(x)图象上是否存在点B(x2,y2)(x2>2),使A、B连线平行于x轴,并说明理由.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 满足
满足 ,且
,且 的最小值
的最小值 ,又函数
,又函数 。
。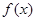 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若 ,求
,求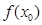 的最小值;
的最小值; ),
), 时,探求函数
时,探求函数 (
( )(
)( ),使
),使 、
、 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…) 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数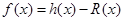 。
。 的单调区间;
的单调区间; ≤
≤ 时,若
时,若 ,求
,求 的最小值;
的最小值; ),当
),当 时,探求函数
时,探求函数 )(
)( ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。