题目内容
已知定义在R上的二次函数f(x)=ax2-2bx+3(1)如果a是集合{1,2,3,4}中的任一元素,b是集合{0,2,3}中的任一元素,试求函数f(x)在区间[1,+∞)上单调递增的概率,
(2)如果a是从区间[1,4]上任取一个数,b是从区间[0,3]上任取一个数,试求函数f(x)在区间[1,+∞)上单调递增的概率.
分析:(1)基本事件有(1,0),(1,2),(1,3),(2,0),(2,2),(2,3),(3,0),(3,2)(3,3),(4,0),(4,2),(4,3)共12个,满足条件的基本事件有9个,由此能求出其概率.
(2)这是一个几何概型,作出图形,能求出其概率.
(2)这是一个几何概型,作出图形,能求出其概率.
解答: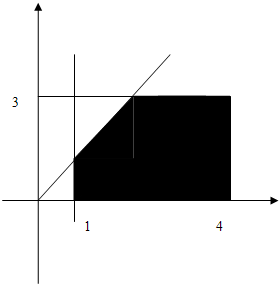 解:(1)有题意知基本事件有(1,0),(1,2),(1,3),(2,0),(2,2),(2,3),(3,0),(3,2)(3,3),(4,0),(4,2),(4,3)共12个,
解:(1)有题意知基本事件有(1,0),(1,2),(1,3),(2,0),(2,2),(2,3),(3,0),(3,2)(3,3),(4,0),(4,2),(4,3)共12个,
要使得方程在[1,+∞)上单调递增,只需对称轴x=
≤1,即a≥b,满足条件的基本事件有9个,所以概率为
=0.75.
(2)这是一个几何概型,如图,所以概率为
=
.
 解:(1)有题意知基本事件有(1,0),(1,2),(1,3),(2,0),(2,2),(2,3),(3,0),(3,2)(3,3),(4,0),(4,2),(4,3)共12个,
解:(1)有题意知基本事件有(1,0),(1,2),(1,3),(2,0),(2,2),(2,3),(3,0),(3,2)(3,3),(4,0),(4,2),(4,3)共12个,要使得方程在[1,+∞)上单调递增,只需对称轴x=
| b |
| a |
| 9 |
| 12 |
(2)这是一个几何概型,如图,所以概率为
3×3-
| ||
| 3×3 |
| 7 |
| 9 |
点评:本题考查概率和函数的综合运用,第(1)题要注意古典概率的运算,第(2)题要注意几何概型的应用.

练习册系列答案
相关题目
 满足
满足 ,且
,且 的最小值
的最小值 ,又函数
,又函数 。
。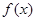 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若 ,求
,求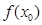 的最小值;
的最小值; ),
), 时,探求函数
时,探求函数 (
( )(
)( ),使
),使 、
、 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…) 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数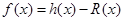 。
。 的单调区间;
的单调区间; ≤
≤ 时,若
时,若 ,求
,求 的最小值;
的最小值; ),当
),当 时,探求函数
时,探求函数 )(
)( ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。