题目内容
已知 是函数
是函数 的极值点.
的极值点.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 R时,函数
R时,函数
 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
 是函数
是函数 的极值点.
的极值点.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)当
 R时,函数
R时,函数
 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.见解析
函数 的极值点求出导数,代入极值点,
的极值点求出导数,代入极值点,
导数为0,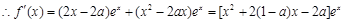
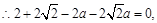 求出a, 求函数
求出a, 求函数 的单调区间时,令导数
的单调区间时,令导数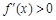 及
及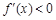 即可解得;函数
即可解得;函数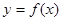 的图象与直线
的图象与直线 有两个不同的交点,由(1)知函数的单调性,数形结合求解(Ⅰ)
有两个不同的交点,由(1)知函数的单调性,数形结合求解(Ⅰ)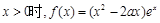 ,
,
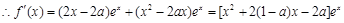 .………………1分
.………………1分
由已知得,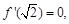
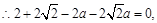 解得a=1. ……………………3分
解得a=1. ……………………3分
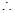
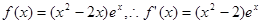 .
.
当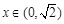 时,
时,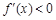 ,当
,当 时,
时,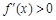 .又
.又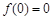 ,………6分
,………6分
当 时,
时, 在
在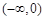 ,
,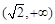 上单调递增,在
上单调递增,在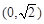 上单调递减. …………7分(Ⅱ)由(1)知,当
上单调递减. …………7分(Ⅱ)由(1)知,当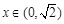 时,
时,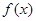 单调递减,
单调递减,
当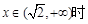 ,
,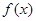 单调递增,
单调递增,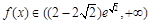 . ………………2分
. ………………2分
(Ⅱ)要使函数
 有两个零点,则函数
有两个零点,则函数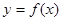 的图象与直线
的图象与直线 有两个不同的交点.①当
有两个不同的交点.①当 时,m=0或
时,m=0或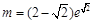 ;………………4分
;………………4分
②当b=0时,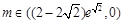 ; ………………5分
; ………………5分
③当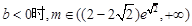
 的极值点求出导数,代入极值点,
的极值点求出导数,代入极值点,导数为0,
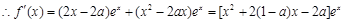
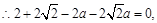 求出a, 求函数
求出a, 求函数 的单调区间时,令导数
的单调区间时,令导数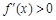 及
及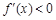 即可解得;函数
即可解得;函数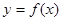 的图象与直线
的图象与直线 有两个不同的交点,由(1)知函数的单调性,数形结合求解(Ⅰ)
有两个不同的交点,由(1)知函数的单调性,数形结合求解(Ⅰ)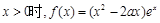 ,
,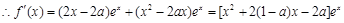 .………………1分
.………………1分 由已知得,
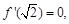
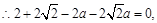 解得a=1. ……………………3分
解得a=1. ……………………3分
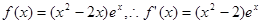 .
.当
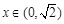 时,
时,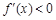 ,当
,当 时,
时,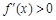 .又
.又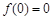 ,………6分
,………6分当
 时,
时, 在
在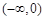 ,
,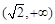 上单调递增,在
上单调递增,在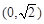 上单调递减. …………7分(Ⅱ)由(1)知,当
上单调递减. …………7分(Ⅱ)由(1)知,当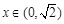 时,
时,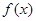 单调递减,
单调递减,
当
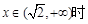 ,
,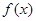 单调递增,
单调递增,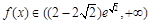 . ………………2分
. ………………2分(Ⅱ)要使函数

 有两个零点,则函数
有两个零点,则函数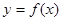 的图象与直线
的图象与直线 有两个不同的交点.①当
有两个不同的交点.①当 时,m=0或
时,m=0或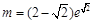 ;………………4分
;………………4分②当b=0时,
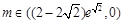 ; ………………5分
; ………………5分③当
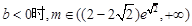

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 在区间
在区间 内函数的导数为正,且
内函数的导数为正,且 ≤0,则函数
≤0,则函数 则
则
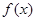 在定义域内存在区间
在定义域内存在区间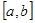 ,满足
,满足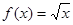 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出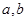 ;若不是,说明理由;
;若不是,说明理由;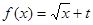 为“优美函数”,求实数
为“优美函数”,求实数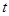 的取值范围.
的取值范围.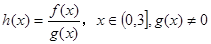 ,对任意
,对任意 恒成立,则( ).
恒成立,则( ). 满足:对任意
满足:对任意 则下述式子中正确的是( )。
则下述式子中正确的是( )。


 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则 是奇函数,且
是奇函数,且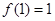 .若
.若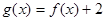 ,则
,则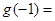 .
.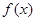 对于区间D内任意的
对于区间D内任意的 ,有
,有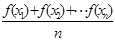
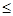
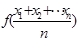 成立,称
成立,称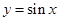 在区间
在区间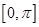 上是“凸函数”,则在△
上是“凸函数”,则在△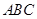 中,
中,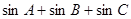 的最大值是( )
的最大值是( )


