题目内容
已知函数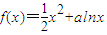
，且f（x）在区间[1，e]（e为自然对数的底数）上的最大值为
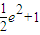，求a的值．
【答案】分析：先求导函数，然后讨论a的值，分别研究函数f（x）在区间[1，e]上的单调性，求出函数的最值，建立等量关系即可求出a的值．
解答：解：f'（x）=x+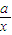
当a=0时，f'（x）＞0∴f（x）在区间[1，e]上的最大值为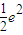
，不符合题意
当a＜0时，f'（x）=0，解得x=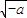
，当
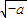≤1时不合题意，当1＜
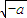＜e，时也不合题意，当
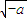＞e也不合题意．
当a＞0时，f'（x）＞0∴f（x）在区间[1，e]上的最大值为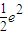
+a，
而f（x）在区间[1，e]（e为自然对数的底数）上的最大值为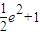
，
∴a=1即a的值为1．
点评：本题主要考查了利用导数求闭区间上函数的最值，以及分类讨论的数学思想，属于基础题．
解答：解：f'（x）=x+
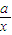
当a=0时，f'（x）＞0∴f（x）在区间[1，e]上的最大值为
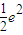，不符合题意当a＜0时，f'（x）=0，解得x=
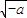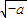，当≤1时不合题意，当1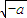＜＜e，时也不合题意，当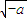＞e也不合题意．当a＞0时，f'（x）＞0∴f（x）在区间[1，e]上的最大值为
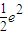+a，而f（x）在区间[1，e]（e为自然对数的底数）上的最大值为
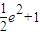，∴a=1即a的值为1．
点评：本题主要考查了利用导数求闭区间上函数的最值，以及分类讨论的数学思想，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
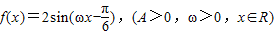，且f（x）的最小正周期是2π．
，
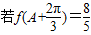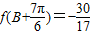，求sinC的值．
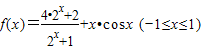，且f（x）存在最大值M和最小值N，则M、N一定满足（ ）
，且f（x）=3，则x= ．
，且f（x）=3，则x= ．