题目内容
三棱锥S-ABC中,SA⊥底面ABC,SA=4,AB=3,G为底面三角形ABC的重心,∠ABC=90°,则点G到面SBC的距离等于分析:先取AB的中点D,连DG,由DG∥面SBC,点G到面SBC的距离等于点D到面SBC的距离.由面面垂直的性质找出点D到面SBC的距离DE,再利用三角形相似,对应边成比例求出DE的值.
解答:解:取AB的中点D,连DG,由DG∥面SBC,
点G到面SBC的距离等于点D到面SBC的距离.
∵SA⊥底面ABC,SA=4,AB=3,D为AB的中点,∠ABC=90°,
∴BC⊥面SAB∴面 SBC⊥面SAB,在面SAB中,作DE⊥SB,
则 DE⊥面SBC,DE为所求.
由△BDE∽△BSA 得:
=
即
=
,
∴DE=
故答案为:
.
点G到面SBC的距离等于点D到面SBC的距离.
∵SA⊥底面ABC,SA=4,AB=3,D为AB的中点,∠ABC=90°,
∴BC⊥面SAB∴面 SBC⊥面SAB,在面SAB中,作DE⊥SB,
则 DE⊥面SBC,DE为所求.
由△BDE∽△BSA 得:
| DE |
| SA |
| BD |
| BS |
| DE |
| 4 |
| ||
| 5 |
∴DE=
| 6 |
| 5 |
故答案为:
| 6 |
| 5 |
点评:本题考查点、线、面间的距离计算、线面垂直、面面垂直性质的应用.属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
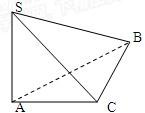 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,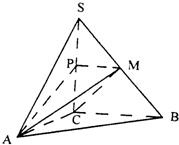 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形,
如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2