题目内容
函数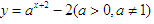 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线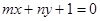 上,其中
上,其中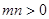 ,则
,则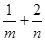 的最小值为 .
的最小值为 .
8
解析试题分析:根据题意,由于函数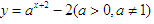 的图象恒过定点A,即为x=-2,y=-1,故A(-2,-1),因为点A在直线
的图象恒过定点A,即为x=-2,y=-1,故A(-2,-1),因为点A在直线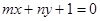 ,则可知2m+n-1=0,则由于
,则可知2m+n-1=0,则由于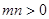 ,可知m,n都是正数,则结合均值不等式可知
,可知m,n都是正数,则结合均值不等式可知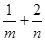
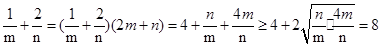 ,当且仅当n=2m时成立,故可知最小值为8,答案为8.
,当且仅当n=2m时成立,故可知最小值为8,答案为8.
考点:指数函数性质以及不等式求解最值
点评:解决关键是确定出定点,然后结合不等式的思想来求解最值,属于中档题。

练习册系列答案
相关题目
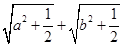 的取值范围是 .
的取值范围是 . 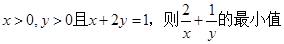 为
为 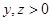 ,且
,且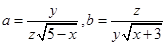 ,记
,记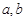 中的最大数为
中的最大数为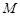 ,则
,则 的值最小, 则这两个正数的积等于 .
的值最小, 则这两个正数的积等于 .  满足
满足 ,则
,则 的最小值为_____________.
的最小值为_____________.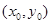 在直线
在直线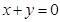 上运动时,
上运动时,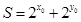 的最小值是
的最小值是 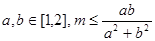 恒成立,则m的最大值是
恒成立,则m的最大值是 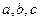 为正数,且
为正数,且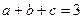 ,则
,则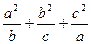 的最小值是__________.
的最小值是__________.