题目内容
若对任意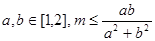 恒成立,则m的最大值是
恒成立,则m的最大值是
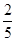
解析试题分析:因为 ,令z=
,令z=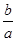 . 作出
. 作出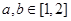 表示的平面区域,可知
表示的平面区域,可知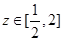 ,所以
,所以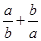 的最大值为
的最大值为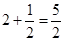 ,所以
,所以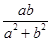 的最小值为
的最小值为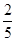 ,所以
,所以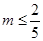 ,所以m的最大值是
,所以m的最大值是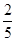 .
.
考点:简单的线性规划,斜率的几何意义,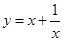 的单调性与最值.
的单调性与最值.
点评:本小题看似是一个不等式恒成立问题,实质是一个与线性规划结合的一个函数最值题,关键是把式子 ,然后令z=
,然后令z=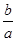 .根据
.根据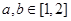 ,结合z的几何意义可求出z的范围,然后求出
,结合z的几何意义可求出z的范围,然后求出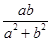 的最小值为
的最小值为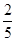 ,问题得解。
,问题得解。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
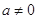 直线
直线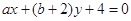 与直线
与直线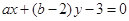 互相垂直,则
互相垂直,则 的最大值为 .
的最大值为 .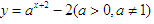 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线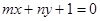 上,其中
上,其中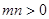 ,则
,则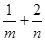 的最小值为 .
的最小值为 .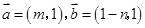 ,且
,且 ,则
,则 的最小值是
的最小值是  ,且
,且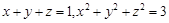 ,则
,则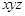 的最大值为
的最大值为 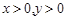 ,且
,且 ,则
,则 的最大值为 .
的最大值为 .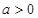 ,
,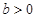 ,且
,且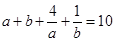 ,则
,则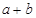 最大值是________。
最大值是________。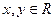 ,则
,则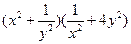 的最小值为 ;
的最小值为 ;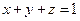 ,则
,则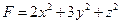 的最小值为_____________。
的最小值为_____________。