Question

（09 年聊城一模理）（12分）                       

如图，在四棱台ABCD―A₁B₁C₁D₁中，下底ABCD是边长

为2的正方形，上底A₁B₁C₁D₁是边长为1的正方形，

侧棱DD₁⊥平面ABCD，DD₁=2.

（Ⅰ）求证：平面；

（II）（理）求二面角的余弦值.

（文）求证：平面⊥平面B₁BDD₁.

Answer 1

解析：以D为原点，以DA、DC、DD₁所在直线分别为x轴，z轴建立空间直角坐标系D―xyz如图，则有A（2，0，0），B（2，2，0），C（0，2，0），A₁（1，0，2），B₁（1，1，2），C₁（0，1，2），D₁（0，0，2）. …  3分

（Ⅰ）证明：设则有所以，，∴平面；………6分

（II）解：

设为平面的法向量，

于是………8分

同理可以求得平面的一个法向量，………10分

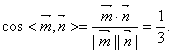
∴二面角的余弦值为. ………12分