题目内容
给出下列命题:“p:?x∈(0,+∞),不等式ax≤x2-a恒成立”;q:“1是x的不等式(x-a)(x-a-1)≤0的解”.若两命题中有且只有一个是真命题,则实数a的取值范围是________.
(-∞,0)∪(0,1]
分析:通过解决二次不等式恒成立求出p是真命题时a的范围,通过解二次不等式求出q是真命题时a的范围,“有且仅有一个真”
分两类求出a的范围.
解答:若p真,则有a≤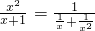 ,由于
,由于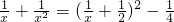 在x∈(0,+∞)上是个减函数,
在x∈(0,+∞)上是个减函数,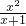 是个增函数,又当x趋向于0时,它的函数值趋向于无穷大,此时
是个增函数,又当x趋向于0时,它的函数值趋向于无穷大,此时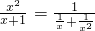 的值趋向于0,但不可能取到0,所以a≤0
的值趋向于0,但不可能取到0,所以a≤0
若q真则有(1-a)(1-a-1)≤0解得0≤a≤1
∵两命题中有且只有一个是真命题
则①p真q假时,有a<0
②p假q真时,有0<a≤1
综上知a∈(-∞,0)∪(0,1]
故答案为(-∞,0)∪(0,1]
点评:本题考查二次不等式恒成立求参数范围、二次不等式的解法、分类讨论的数学思想方法.
分析:通过解决二次不等式恒成立求出p是真命题时a的范围,通过解二次不等式求出q是真命题时a的范围,“有且仅有一个真”
分两类求出a的范围.
解答:若p真,则有a≤
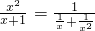 ,由于
,由于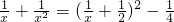 在x∈(0,+∞)上是个减函数,
在x∈(0,+∞)上是个减函数,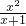 是个增函数,又当x趋向于0时,它的函数值趋向于无穷大,此时
是个增函数,又当x趋向于0时,它的函数值趋向于无穷大,此时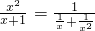 的值趋向于0,但不可能取到0,所以a≤0
的值趋向于0,但不可能取到0,所以a≤0若q真则有(1-a)(1-a-1)≤0解得0≤a≤1
∵两命题中有且只有一个是真命题
则①p真q假时,有a<0
②p假q真时,有0<a≤1
综上知a∈(-∞,0)∪(0,1]
故答案为(-∞,0)∪(0,1]
点评:本题考查二次不等式恒成立求参数范围、二次不等式的解法、分类讨论的数学思想方法.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;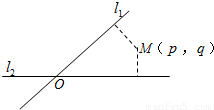 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;