题目内容
设函数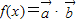 ,其中向量
,其中向量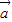 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点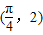 .
.(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合.
【答案】分析:(Ⅰ)利用向量的数量积化简函数的表达式,通过函数的图象经过点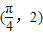 ,求实数m的值;
,求实数m的值;
(Ⅱ)通过(Ⅰ)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求函数f(x)的最小值及此时x值的集合.
解答:解:(Ⅰ)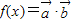 =m(1+sin2x)+cos2x,…(3分)
=m(1+sin2x)+cos2x,…(3分)
由已知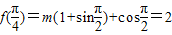 ,得m=1.…(6分)
,得m=1.…(6分)
(Ⅱ)由(Ⅰ)得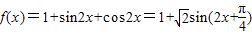 ,…(9分)∴当
,…(9分)∴当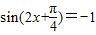 时,f(x)的最小值为
时,f(x)的最小值为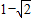 ,…(11分)
,…(11分)
由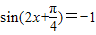 ,得x值的集合为
,得x值的集合为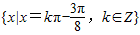 .…(14分)
.…(14分)
点评:本题是中档题,考查向量的数量积与三角函数的化简求值,考查计算能力.常考题型.
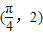 ,求实数m的值;
,求实数m的值;(Ⅱ)通过(Ⅰ)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求函数f(x)的最小值及此时x值的集合.
解答:解:(Ⅰ)
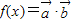 =m(1+sin2x)+cos2x,…(3分)
=m(1+sin2x)+cos2x,…(3分)由已知
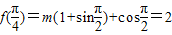 ,得m=1.…(6分)
,得m=1.…(6分)(Ⅱ)由(Ⅰ)得
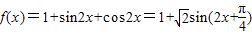 ,…(9分)∴当
,…(9分)∴当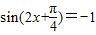 时,f(x)的最小值为
时,f(x)的最小值为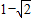 ,…(11分)
,…(11分)由
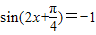 ,得x值的集合为
,得x值的集合为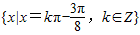 .…(14分)
.…(14分)点评:本题是中档题,考查向量的数量积与三角函数的化简求值,考查计算能力.常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
. ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R. ,
, =(m,n)(|m|<
=(m,n)(|m|<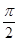 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值. ,其中向量
,其中向量 ,
, ,
, ,且
,且 的图象经过点
的图象经过点 .(1)求实数
.(1)求实数 的值;
的值; 的最小值及此时
的最小值及此时 值的集合.
值的集合.