题目内容
(本题满分12分)设函数 ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,
 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- 且x∈[-
且x∈[- ,
, ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量 =(m,n)(|m|<
=(m,n)(|m|<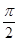 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
【答案】
解:(1)依题设,f(x)=2cos2x+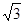 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+ ). ……………2分
). ……………2分
由1+2sin(2x+ )=1-
)=1-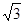 ,得sin(2x+
,得sin(2x+ )=-
)=-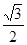 .……………4分
.……………4分
∵-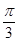 ≤x≤
≤x≤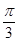 ,∴-
,∴-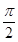 ≤2x+
≤2x+ ≤
≤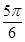 ,∴2x+
,∴2x+ =-
=-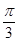 ,
,
即x=-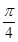 .
.……………6分
.
.……………6分
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
即函数y=f(x)的图象. .……………8分
由(1)得 f(x)=2sin2(x+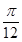 )+1. ∵|m|<
)+1. ∵|m|<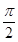 ,∴m=-
,∴m=-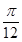 ,n=1. .……………12分
,n=1. .……………12分
【解析】略

练习册系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;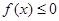 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求