题目内容
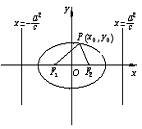
设P(x0,y0)是离心率为e的椭圆,方程为![]() 上的一点,P到左焦点F1和右焦点F2的距离分别为r1和r2。求证:r1=a+ex0,r2=a-ex0。
上的一点,P到左焦点F1和右焦点F2的距离分别为r1和r2。求证:r1=a+ex0,r2=a-ex0。
答案:
解析:
解析:
证明:
由椭圆第二定义,得
∴|PF1|=e ∴|PF1|=a+ex0 又 ∴|PF2|=e ∴|PF2|=a-ex0。 |

练习册系列答案
相关题目
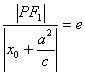
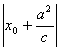 =e
=e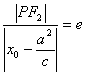
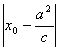 =e
=e