题目内容
已知椭圆中心在坐标原点,焦点在坐标轴上,直线y=x+1和椭圆交于P、Q两点,且![]() 求椭圆方程。
求椭圆方程。
设椭圆方程为![]()
![]()
![]() ??
??
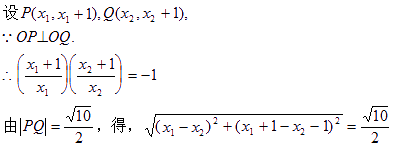
![]() ??
??
![]() ??
??
这里![]() 是方程??的实根,由韦达定理,
是方程??的实根,由韦达定理,
![]() ??
??
![]() ??
??
把??、??代入??、??得,
![]() =2,
=2,
![]()
消去m得,4n2-8n+3=0
解得: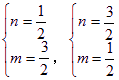
![]()
解析:
椭圆的焦点在x轴上时,方程为![]() 焦点在y轴上时,方程为
焦点在y轴上时,方程为![]() 求这两个方程,实质上是求x2,y2的系数,因此设椭圆方程为
求这两个方程,实质上是求x2,y2的系数,因此设椭圆方程为![]() 既概括了两种不同位置,且方程又是整式,给计算带来方便。
既概括了两种不同位置,且方程又是整式,给计算带来方便。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
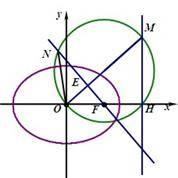 已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2.
已知椭圆中心在坐标原点,短轴长为2,一条准线l的方程为x=2. 在坐标原点,焦点在
在坐标原点,焦点在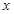 轴上,且经过
轴上,且经过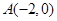 、
、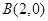 、
、 三点.
三点.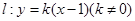 与椭圆
与椭圆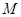 、
、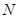 两点.
两点.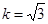 ,求
,求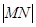 的长;
的长; 与直线
与直线 的交点在直线
的交点在直线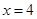 上.
上.