题目内容
(本题满分13分)
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
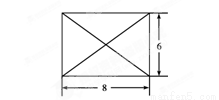
(1)求该几何体的体积V. (2)求该几何体的侧面积S.
【答案】
解:(1)V=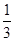 ×8×6×4=64.
×8×6×4=64.
(2)
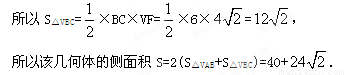
【解析】本题考查三视图求面积、体积,考查空间想象能力,是基础题
(1)由题意可知该几何体是四棱锥,求出底面积和高即可求解.
(2)因为OE⊥AB,OF⊥BC,那么利用已知条件得到侧面的三角形的面积得到结论。
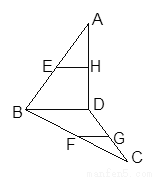
解:(1)由该几何体的俯视图、正视图、侧视图可知,该几何体是四棱锥,且四棱锥的底面ABCD是边长为6和8的矩形,高VO=4,O点是AC与BD的交点.
所以该几何体的体积V=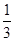 ×8×6×4=64.
×8×6×4=64.
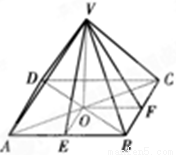
(2)如图所示,OE⊥AB,OF⊥BC,
在侧面VAB中,VE=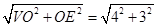 =5,所以S△VAB=
=5,所以S△VAB=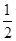 ×AB×VE=
×AB×VE=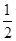 ×8×5=20.
×8×5=20.
在侧面VBC中,VF=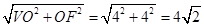 ,
,
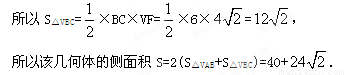

练习册系列答案
相关题目
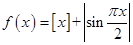 ,
,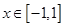 .其中
.其中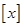 表示不超过
表示不超过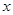 的最大整数,例如
的最大整数,例如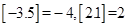 .
.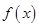 的奇偶性,并说明理由;
的奇偶性,并说明理由;