题目内容
已知椭圆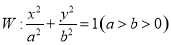 的离心率为
的离心率为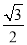 ,其左顶点
,其左顶点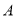 在圆
在圆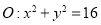 上.
上.
(Ⅰ)求椭圆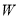 的方程;
的方程;
(Ⅱ)若点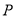 为椭圆
为椭圆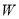 上不同于点
上不同于点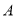 的点,直线
的点,直线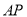 与圆
与圆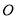 的另一个交点为
的另一个交点为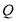 ,是否存在点
,是否存在点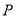 ,使得
,使得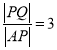 ?若存在,求出点
?若存在,求出点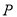 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
题目内容
已知椭圆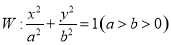 的离心率为
的离心率为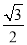 ,其左顶点
,其左顶点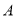 在圆
在圆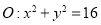 上.
上.
(Ⅰ)求椭圆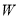 的方程;
的方程;
(Ⅱ)若点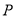 为椭圆
为椭圆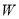 上不同于点
上不同于点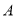 的点,直线
的点,直线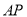 与圆
与圆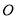 的另一个交点为
的另一个交点为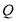 ,是否存在点
,是否存在点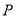 ,使得
,使得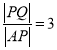 ?若存在,求出点
?若存在,求出点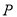 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案