题目内容
设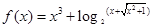 ,则对任意实数a,b,a+b
,则对任意实数a,b,a+b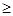 0是
0是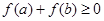 的( )
的( )
| A.充要条件 | B.充要不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
A
解析试题分析:由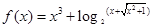
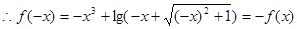
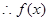 是奇函数.∴f(x)为增函数.∵a+b≥0,⇒a≥-b,∴f(a)≥f(-b),∴f(a)≥-f(b),
是奇函数.∴f(x)为增函数.∵a+b≥0,⇒a≥-b,∴f(a)≥f(-b),∴f(a)≥-f(b),
∴f(a)+f(b)≥0,反之也成立,∴“a+b≥0”是“f(a)+f(b)≥0”的充要条件,选A.
考点:1.利用函数的导数判断函数的单调性;2.充要条件

练习册系列答案
相关题目
命题“已知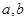 为实数,若
为实数,若 ,则
,则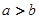 ”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
| A.0 | B.1 | C.2 | D.4 |
命题“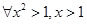 ” 的否定是( )
” 的否定是( )
A.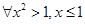 | B. |
C.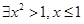 | D.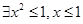 |
命题“存在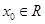 使得
使得 ”的否定是( )
”的否定是( )
A.不存在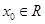 使得 使得 | B.对任意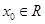 , , |
C.对任意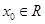 , , | D.存在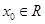 ,使得 ,使得 |
给出命题:已知 为实数,若
为实数,若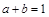 ,则
,则 .在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
.在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
“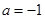 ”是“直线
”是“直线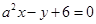 与直线
与直线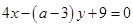 互相垂直”的( )
互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题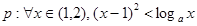 恒成立;命题
恒成立;命题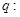 方程
方程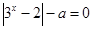 有两个实数根,则命题
有两个实数根,则命题 是命题
是命题 成立的( )条件
成立的( )条件
| A.充分而不必要 | B.必要而不充分 |
| C.充要 | D.既不充分也不必要 |
已知函数 ,其中
,其中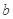 为常数.那么“
为常数.那么“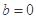 ”是“
”是“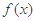 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题p:?x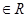 ,
,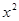 >0,则( )
>0,则( )
A.非p:?x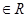 , ,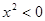 | B.非p:?x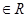 , , |
C.非p:?x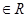 , , | D.非p:?x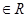 , ,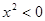 |