题目内容
函数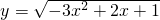 的单调递减区间为
的单调递减区间为
- A.

- B.
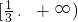
- C.
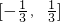
- D.

D
分析:本题先要求出函数的定义域,然后利用复合函数的单调性概念,求出内函数的单调区间,复合函数求单调区间时要对内外函数的增减关系加以注意,即“同增异减”,本题先求出定义域为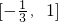 ,而内函数u=-3x2+2x+1=-3(x-
,而内函数u=-3x2+2x+1=-3(x- )2+
)2+ ,从而得内函数单调减区间为[
,从而得内函数单调减区间为[ ,+∞).
,+∞).
解答:由已知:-3x2+2x+1≥0,
所以3x2-2x-1≤0,得:
所以函数的定义域为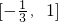
设u=-3x2+2x+1=-3(x- )2+
)2+ ,则
,则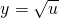
因为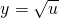 是增函数,所以由u=-3x2+2x+1=-3(x-
是增函数,所以由u=-3x2+2x+1=-3(x- )2+
)2+ 的单调减区间为[
的单调减区间为[ ,+∞)
,+∞)
又因为函数的定义域为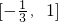 ,所以函数的单调减区间为
,所以函数的单调减区间为 
故应选:D
点评:本题考查了函数的定义域及其求法,二次不等式解集的求法,复合函数单调性的判断,单调区间的求法..
分析:本题先要求出函数的定义域,然后利用复合函数的单调性概念,求出内函数的单调区间,复合函数求单调区间时要对内外函数的增减关系加以注意,即“同增异减”,本题先求出定义域为
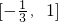 ,而内函数u=-3x2+2x+1=-3(x-
,而内函数u=-3x2+2x+1=-3(x- )2+
)2+ ,从而得内函数单调减区间为[
,从而得内函数单调减区间为[ ,+∞).
,+∞).解答:由已知:-3x2+2x+1≥0,
所以3x2-2x-1≤0,得:

所以函数的定义域为
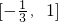
设u=-3x2+2x+1=-3(x-
 )2+
)2+ ,则
,则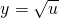
因为
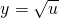 是增函数,所以由u=-3x2+2x+1=-3(x-
是增函数,所以由u=-3x2+2x+1=-3(x- )2+
)2+ 的单调减区间为[
的单调减区间为[ ,+∞)
,+∞)又因为函数的定义域为
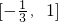 ,所以函数的单调减区间为
,所以函数的单调减区间为 
故应选:D
点评:本题考查了函数的定义域及其求法,二次不等式解集的求法,复合函数单调性的判断,单调区间的求法..

练习册系列答案
相关题目
 上任一点
上任一点 处的切线斜率
处的切线斜率 ,则该函数的单调递减区间为 .
,则该函数的单调递减区间为 . 的单调递减区间为____________,增区间为_______________.
的单调递减区间为____________,增区间为_______________.