题目内容
已知两个实数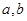 满足
满足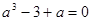 且
且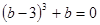 ,则
,则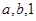 三个数从小到大的关系是 (用“
三个数从小到大的关系是 (用“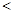 ”表示).
”表示).
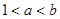
解析试题分析:
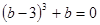 ,
,
 ,由下面图象知函数
,由下面图象知函数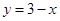 的图象与
的图象与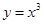 与
与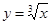 的图像交点的横坐标分别为
的图像交点的横坐标分别为 、
、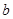 ,故
,故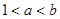 .
.
考点:函数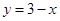 、与、
、与、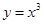 及
及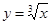 的图象性质.
的图象性质.

练习册系列答案
相关题目
题目内容
已知两个实数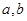 满足
满足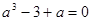 且
且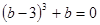 ,则
,则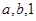 三个数从小到大的关系是 (用“
三个数从小到大的关系是 (用“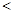 ”表示).
”表示).
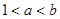
解析试题分析:
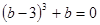 ,
,
 ,由下面图象知函数
,由下面图象知函数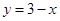 的图象与
的图象与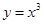 与
与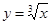 的图像交点的横坐标分别为
的图像交点的横坐标分别为 、
、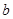 ,故
,故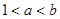 .
.
考点:函数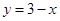 、与、
、与、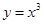 及
及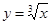 的图象性质.
的图象性质.
