题目内容
已知关于x的方程x2+(m+2)x+m=0.
(1)若该方程有一个正根和一个负根,且负根的绝对值较大,求实数m的取值范围.
(2)是否存在实数m,使方程的一个根在区间(0,1)内,另一个根在区间(3,4)内?若存在,求出实数m的取值范围;若不存在,请说明理由.
答案:
解析:
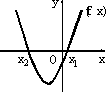
解析:
解:令f(x)=x2+(m+2)x+m,其图象的对称轴为x=-![]() .
.
(1)因为方程x2+(m+2)x+m=0有两个根,所以函数f(x)=x2+(m+2)·x+m有两个零点,记为x1,x2.由题意,不妨设x1>0,x2<0,且|x1|<|x2|,函数f(x)的图象如图所示,则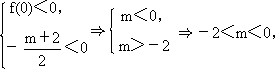 所以,实数m的取值范围是(-2,0).
所以,实数m的取值范围是(-2,0).
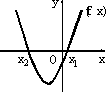
(2)假设存在实数m,使方程的一个根在区间(0,1)内,另一个根在区间(3,4)内,即函数f(x)=x2+(m+2)x+m的两个零点分别在区间(0,1),(3,4)内,结合函数图象,可得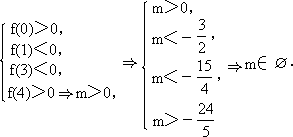 所以不存在这样的实数m.
所以不存在这样的实数m.

练习册系列答案
相关题目