题目内容
已知函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,在曲线
时,在曲线 上是否存在两点
上是否存在两点 ,使得曲线在
,使得曲线在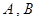 两点处的切线均与直线
两点处的切线均与直线 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
(Ⅲ)若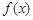 在区间
在区间 存在最大值
存在最大值 ,试构造一个函数
,试构造一个函数 ,使得
,使得 同时满足以下三个条件:①定义域
同时满足以下三个条件:①定义域 ,且
,且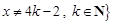 ;②当
;②当 时,
时, ;③在
;③在 中使
中使 取得最大值
取得最大值 时的
时的 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数 即可)
即可)
(Ⅰ)详见解析;(Ⅱ)存在,且交点纵坐标的取值范围是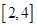 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)对参数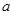 的值影响函数极值点的存在与否进行分类讨论,结合求解导数不等式求相应的单调区间;(Ⅱ)先将曲线在点
的值影响函数极值点的存在与否进行分类讨论,结合求解导数不等式求相应的单调区间;(Ⅱ)先将曲线在点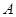 、
、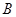 处的切线方程求出,并将交点的坐标假设出来,利用交点坐标满足两条切线方程,得到两个不同的等式,然后利用等式的结构进行相应转化为函数的零点个数来处理;(Ⅲ)可以根据题中的条件进行构造,但要注意定义域等相应问题.
处的切线方程求出,并将交点的坐标假设出来,利用交点坐标满足两条切线方程,得到两个不同的等式,然后利用等式的结构进行相应转化为函数的零点个数来处理;(Ⅲ)可以根据题中的条件进行构造,但要注意定义域等相应问题.
试题解析:(Ⅰ)依题可得 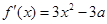 ,
,
当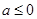 时,
时,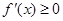 恒成立,函数
恒成立,函数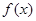 在
在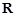 上单调递增;
上单调递增;
当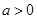 时,由
时,由 ,解得
,解得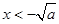 或
或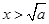 ,
,
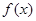 单调递增区间为
单调递增区间为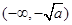 和
和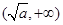 .
4分
.
4分
(Ⅱ)设切线与直线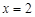 的公共点为
的公共点为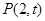 ,当
,当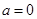 时,
时,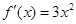 ,
,
则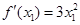 ,因此以点
,因此以点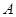 为切点的切线方程为
为切点的切线方程为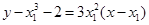 .
.
因为点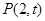 在切线上,所以
在切线上,所以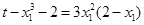 ,即
,即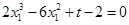 .
.
同理可得方程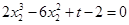 .
6分
.
6分
设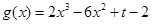 ,则原问题等价于函数
,则原问题等价于函数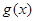 至少有两个不同的零点.
至少有两个不同的零点.
因为 ,
,
当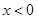 或
或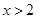 时,
时,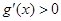 ,
,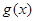 单调递增,当
单调递增,当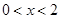 时,
时,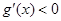 ,
,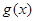 单调递减.
单调递减.
因此,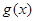 在
在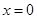 处取极大值
处取极大值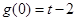 ,在
,在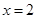 处取极小值
处取极小值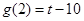 .
.
若要满足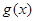 至少有两个不同的零点,则需满足
至少有两个不同的零点,则需满足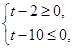 解得
解得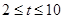 .
.
故存在,且交点纵坐标的取值范围为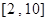 . 10分
. 10分
(Ⅲ)由(Ⅰ)知,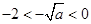 ,即
,即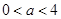 . 11分
. 11分
本题答案不唯一,以下几个答案供参考:
①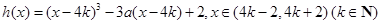 ,其中
,其中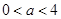 ;
;
②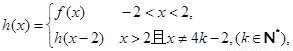 其中
其中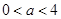 ;
;
③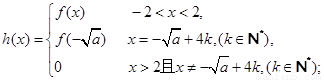 其中
其中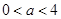 . 14分
. 14分
考点:函数的单调区间、函数的零点

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 .
. 上的最大值和最小值.
上的最大值和最小值. .
. 成立的
成立的 的取值范围;
的取值范围; 时,求函数
时,求函数 的值域.
的值域. .
. 的单调区间;
的单调区间; 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间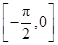 上的最小值和最大值.
上的最小值和最大值. .
. 的最小正周期及最值;
的最小正周期及最值; ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.