题目内容
6.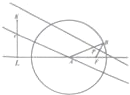 在高中数学课本中我们见过许多的“信息技术应用”,我们可以利用几何画板软件的拖动、动画及计算等功能来研究许多数学问题,比如:在平面内做一条线段KL,以定点A为圆心,以|KL|为半径作一圆,在圆内取一定点F,在圆上取动点B,作线段BF的中垂线与圆A的半径AB交于点P.当点B在圆上运动时,就会发现点P的运动轨迹.
在高中数学课本中我们见过许多的“信息技术应用”,我们可以利用几何画板软件的拖动、动画及计算等功能来研究许多数学问题,比如:在平面内做一条线段KL,以定点A为圆心,以|KL|为半径作一圆,在圆内取一定点F,在圆上取动点B,作线段BF的中垂线与圆A的半径AB交于点P.当点B在圆上运动时,就会发现点P的运动轨迹.(Ⅰ)你能猜出点P的轨迹是什么曲线吗?请说明理由;若|KL|=6,|AF|=4,以线段AF的中点O为原点,以直线AF为x轴,建立平面直角坐标系,试求点P的轨迹方程;
(Ⅱ)在(Ⅰ)的条件下,过点A作直线l与点P的轨迹交于两点M、N,试求线段MN的中点Q的轨迹方程;
(Ⅲ)拖动改变线段KL的长度,会发现点P的轨迹C的形状在发生变化,请问在保持(Ⅰ)中轨迹C类型不变的前提下,当C的离心率e在什么范围变化时,C上总存在点R,使得AR⊥FR?
分析 (Ⅰ)连结PF,通过中垂线的性质及等价代换可知|PA|+|PF|=|KL|,即点P的轨迹是以A、F为焦点的椭圆,计算可得其轨迹方程;
(Ⅱ)由(Ⅰ)可知A(-2,0),将M(x1,y1),N(x2,y2)代入点P的方程,利用中点坐标公式,分x1≠x2、x1=x2两种情况讨论即可;
(Ⅲ)通过设C的方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),作圆:x2+y2=c2(c>0,c2=a2-b2),利用c≥b计算即可.
解答  解:(Ⅰ)结论:点P的轨迹是以点A、F为焦点的椭圆.
解:(Ⅰ)结论:点P的轨迹是以点A、F为焦点的椭圆.
理由如下:
连结PF,由题意可知|PF|=|PB|,
∴|PA|+|PF|=|PA|-|PB|=|AB|=|KL|(定值,且|KL|>|AF|),
由椭圆的定义可知:点P的轨迹是以A、F为焦点的椭圆;
∵|KL|=6,|AF|=4,
∴2a=6,2c=4,即a=3,c=2,
∴b2=a2-c2=5,
∴点P的轨迹方程为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$;
(Ⅱ)由(Ⅰ)可知A(-2,0),设M(x1,y1),N(x2,y2),Q(x,y),
由$\left\{\begin{array}{l}{5{{x}_{1}}^{2}+9{{y}_{1}}^{2}=45}\\{5{{x}_{2}}^{2}+9{{y}_{2}}^{2}=45}\end{array}\right.$,可得:5(x1+x2)(x1-x2)=-9(y1+y2)(y1-y2),
当x1≠x2时,kMN=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$-\frac{5}{9}$•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=$-\frac{5}{9}$•$\frac{x}{y}$,
又∵kMN=kAQ,即$-\frac{5}{9}$•$\frac{x}{y}$=$\frac{y-0}{x+2}$,
∴5x2+9y2+10x=0;
当x1=x2时,x1=x2=-2,
此时Q(-2,0)也满足方程:5x2+9y2+10x=0;
∴线段MN的中点Q的轨迹方程为:5x2+9y2+10x=0;
(Ⅲ)在保持(Ⅰ)中轨迹C类型不变的前提下,C为椭圆,
设其方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
作圆:x2+y2=c2(c>0,c2=a2-b2).
当此圆与椭圆C有公共点时,C上总存在点R,使得AR⊥FR,此时应有c≥b.
∴c2≥b2,∴c2≥a2-c2,
即2c2≥a2,∴e2=$\frac{{c}^{2}}{{a}^{2}}$≥$\frac{1}{2}$,
又∵0<e<1,∴e∈[$\frac{1}{2}$,1).
点评 本题考查轨迹方程,考察椭圆的定义,考查学生分析解决问题的能力,注意解题方法的积累,属于中档题.

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
| A. | {1} | B. | {0} | C. | {0,1} | D. | {-1,0,1} |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
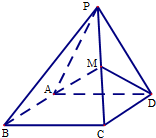 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]).
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为棱PC上的动点,且$\frac{PM}{PC}$=λ(λ∈[0,1]).