题目内容
12.如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,又AD∥BC,AD⊥DC,且PD=BC=3AD=3.(Ⅰ)画出四棱准P-ABCD的正视图;
(Ⅱ)求证:平面PAD⊥平面PCD;
(Ⅲ)求证:棱PB上存在一点E,使得AE∥平面PCD,并求$\frac{PE}{EB}$的值.
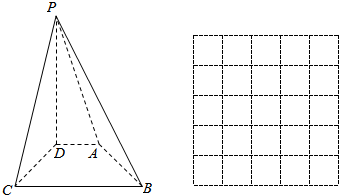
分析 (Ⅰ)画出正视图即可;(Ⅱ)根据面面垂直的判定定理证明即可;(Ⅲ)根据线面垂直的判定定理进行证明即可.
解答 (Ⅰ)解:四棱准P-ABCD的正视图如图所示.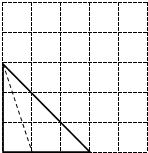 ;
;
(Ⅱ)证明:因为 PD⊥平面ABCD,AD?平面ABCD,
所以 PD⊥AD.
因为 AD⊥DC,PD∩CD=D,PD?平面PCD,CD?平面PCD,
所以AD⊥平面PCD,
因为 AD?平面PAD,
所以 平面PAD⊥平面PCD.
(Ⅲ)分别延长CD,BA交于点O,连接PO,在棱PB上取一点E,使得$\frac{PE}{EB}=\frac{1}{2}$,
下证AE∥平面PCD,
因为 AD∥BC,BC=3AD,
所以 $\frac{OA}{OB}=\frac{AD}{BC}=\frac{1}{3}$,即$\frac{OA}{AB}=\frac{1}{2}$,
所以 $\frac{OA}{AB}=\frac{PE}{EB}$.
所以 AE∥OP,
因为OP?平面PCD,AE?平面PCD,
所以 AE∥平面PCD.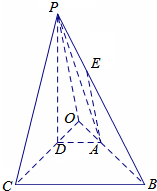
点评 本题考查了三视图问题,考查面面垂直、线面垂直的判断定理,是一道中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
3.设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余,记为a=b(modm).若a=C${\;}_{20}^{0}$+C${\;}_{20}^{1}$+C${\;}_{20}^{2}$+…+C${\;}_{20}^{20}$,a≡b(mod5),则b的值可以是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
20.已知函数f(x)=lnx+$\frac{k}{x}$,k∈R,若f(x)≥2+$\frac{1-e}{x}$恒成立,则实数k的取值范围为( )
| A. | k>1 | B. | k≥1 | C. | k>3 | D. | k≥3 |
5.命题“若x2+y2=0,则x、y全为0”的逆否命题是( )
| A. | 若x、y全为0,则 x2+y2≠0 | B. | 若x、y不全为0,则 x2+y2=0 | ||
| C. | 若x、y全不为0,则 x2+y2≠0 | D. | 若x、y不全为0,则 x2+y2≠0 |
 某校从高一年级男生中随机抽取100个样本,将他们的身高(最高189cm,最低150cm)分成八段:[150,155),[155,160),[160,165),…,[185,190)后得到如图的频率分布直方图.
某校从高一年级男生中随机抽取100个样本,将他们的身高(最高189cm,最低150cm)分成八段:[150,155),[155,160),[160,165),…,[185,190)后得到如图的频率分布直方图.