题目内容
 已知α是第二象限角,且sin(π+α)=
已知α是第二象限角,且sin(π+α)=| k-1 |
| k+1 |
| 5π |
| 2 |
| 3k-1 |
| k+1 |
(1)求角α的正弦值、余弦值和正切值;
(2)在图中作出角α的三角函数线,并用有向线段表示sinα,cosα和tanα.
分析:(1)根据三角函数的诱导公式可得到sinα=-
,cosα=
,由sin2α+cos2α=1可求得k,从而可得角α的正弦值、余弦值和正切值;
(2)根据三角函数中角α正弦线、余弦线与正切线的定义即可作出角α的三角函数线.
| k-1 |
| k+1 |
| 3k-1 |
| k+1 |
(2)根据三角函数中角α正弦线、余弦线与正切线的定义即可作出角α的三角函数线.
解答:解:(1)∵sin(π+α)=-sinα=
,sin(
+α)=cosα=
,
∴sinα=-
,cosα=
,由sin2α+cos2α=1可得:
k=1或k=
;
又α是第二象限角,∴k=
,k=1(舍去),
∴sinα=
,cosα=-
,tanα=-
.
(2)设单位圆与x轴正半轴交于A(1,0),α的终边与单位圆交点为P,过点P向x轴作垂线,垂足为M,
则sinα=MP,cosα=OM,
过A(1,0)作圆的切线与α的终边的反向延长线相交于点T,
tanα=AT.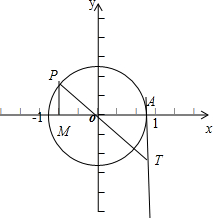
| k-1 |
| k+1 |
| 5π |
| 2 |
| 3k-1 |
| k+1 |
∴sinα=-
| k-1 |
| k+1 |
| 3k-1 |
| k+1 |
k=1或k=
| 1 |
| 9 |
又α是第二象限角,∴k=
| 1 |
| 9 |
∴sinα=
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
(2)设单位圆与x轴正半轴交于A(1,0),α的终边与单位圆交点为P,过点P向x轴作垂线,垂足为M,
则sinα=MP,cosα=OM,
过A(1,0)作圆的切线与α的终边的反向延长线相交于点T,
tanα=AT.

点评:本题考查诱导公式的作用,易错点在于求得k=1或k=
后要根据条件“α是第二象限角”进行验证,属于中档题.
| 1 |
| 9 |

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目

 是第二象限角,
是第二象限角, ,则
,则 = .
= .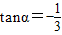 ,则cosα=( )
,则cosα=( )