题目内容
16.下列四个命题①已知命题P:?x∈R,x2+x<0,则?P:?x∈R,x2+x<0;
②$y={x^2}-{({\frac{1}{2}})^x}$的零点所在的区间是(1,2);
③若实数x,y满足xy=1,则x2+2y2的最小值为$2\sqrt{2}$;
④设a,b是两条直线,α,β是两个平面,则a?α,b⊥β,α∥β是a⊥b的充分条件;
其中真命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①利用命题的否定定义即可判断出正误;
②分别画出y=x2与y=$(\frac{1}{2})^{x}$的图象,可知:函数$y={x^2}-{({\frac{1}{2}})^x}$的零点有两个,再利用函数零点存在定理即可判断出;
③利用基本不等式的性质即可判断出正误;
④利用面面平行的性质、线面垂直的性质定理即可判断出正误.
解答 解:①由命题P:?x∈R,x2+x<0,则?P:?x∈R,x2+x≥0,因此不正确;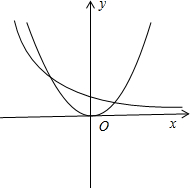
②$y={x^2}-{({\frac{1}{2}})^x}$,分别画出y=x2与y=$(\frac{1}{2})^{x}$的图象,可知:函数$y={x^2}-{({\frac{1}{2}})^x}$的零点有两个:一个零点在区间(0,1),另一个零点-2,因此不正确;
③若实数x,y满足xy=1,则x2+2y2≥$2\sqrt{2xy}$=$2\sqrt{2}$,当且仅当x=$\sqrt{2}$y时取等号,其最小值为$2\sqrt{2}$,正确;
④∵a?α,b⊥β,α∥β,利用面面平行的性质、线面垂直的性质定理可得:a⊥b,反之不成立,因此a?α,b⊥β,α∥β是a⊥b的充分条件,正确.
其中真命题的个数为2.
故选:C.
点评 本题考查了简易逻辑的判定方法、函数的零点、基本不等式的性质、面面平行的性质、线面垂直的性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
6.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2渐近线分别为l1,l2,位于第一象限的点P在l1上,若l2⊥PF1,l2∥PF2,则双曲线的离心率是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
7.设P是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上的任意一点,已知A(a,b),B(a,-b),若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(O为坐标原点),则λ2+μ2的最小值为( )
| A. | $\frac{1}{4}$ab | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ab | D. | $\frac{1}{2}$ |
1.已知抛物线y2=2px(p>0)的焦点F恰好是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点,两条曲线的交点的连线过点F,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |