题目内容
(08年南昌市三校联考文)如图,![]() 的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知
的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知![]() ,
,
![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为L,
,设点A的轨迹为L,
①求L的方程;
②过点C作直线m交曲线L于不同的两点M、N,问在x轴上是否存在一个异于C的定点
Q,使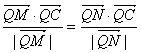 ,对任意的直线m都成立?若存在,试求出点Q的坐标,
,对任意的直线m都成立?若存在,试求出点Q的坐标,
若不存在,请说明理由。

解析:(1)由题知:![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
根据双曲线的定义知,点A的轨迹是以B、C为焦点,实轴长为2的双曲线的右支除去E(1,0),故L的方程为![]() (x>1)
(x>1)
(2)设点Q(x0,0)、M(x1,y)、W(x2、y2)
由(1)可知C(![]() )
)

于是(1)当直线![]() 轴时,点
轴时,点![]() 在x轴任何一点处,都能够使得
在x轴任何一点处,都能够使得![]() 成立
成立
(2)当直线MN不与x轴垂直时,设直线MN:![]()
由 消去y,得
消去y,得
![]()
则![]()
![]()
![]()
![]()
![]()
![]()
所以,要使![]() 成立
成立
要使![]() 成立
成立
即![]() 即
即![]()
即(![]() )
)![]() =
=![]()
![]()
即![]() 即
即![]()
所以,当点Q的坐标为![]() 时,能够使得
时,能够使得 成立
成立


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目