题目内容
(2013•江苏)抛物线y=x2在x=1处的切线与两坐标轴围成三角形区域为D(包含三角形内部和边界).若点P(x,y)是区域D内的任意一点,则x+2y的取值范围是
[-2,
]
| 1 |
| 2 |
[-2,
]
.| 1 |
| 2 |
分析:利用导数求出抛物线在x=1处的切线方程,画出可行域,找出最优解,则x+2y的取值范围可求.
解答: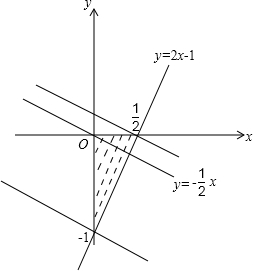 解:由y=x2得,y′=2x,所以y′|x=1=2,则抛物线y=x2在x=1处的切线方程为y=2x-1.
解:由y=x2得,y′=2x,所以y′|x=1=2,则抛物线y=x2在x=1处的切线方程为y=2x-1.
令z=x+2y,则y=-
x+
.
画出可行域如图,
所以当直线y=-
x+
过点(0,-1)时,zmin=-2.
过点(
,0)时,zmax=
.
故答案为[-2,
].
 解:由y=x2得,y′=2x,所以y′|x=1=2,则抛物线y=x2在x=1处的切线方程为y=2x-1.
解:由y=x2得,y′=2x,所以y′|x=1=2,则抛物线y=x2在x=1处的切线方程为y=2x-1.令z=x+2y,则y=-
| 1 |
| 2 |
| z |
| 2 |
画出可行域如图,
所以当直线y=-
| 1 |
| 2 |
| z |
| 2 |
过点(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为[-2,
| 1 |
| 2 |
点评:本题考查了导数的运算,考查了简单的线性规划,解答的关键是把问题转化为线性规划知识解决,是基础题.

练习册系列答案
相关题目