题目内容
A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心,若BC=5,CD=8,∠BCD=60°,则MN的长为分析:本题考查的知识点是余弦定理和平行线分线段成比例定理,由BC=5,CD=8,∠BCD=60°,结合余弦定理,我们易得BD的长,又由M、N分别是△ABC和△ACD的重心,延长AM交BC于P,延长AN交CD于Q,易得PQ为△BCD的中位线,AM:AP=AN:AQ=2:3,将BD长代入即可得到答案.
解答: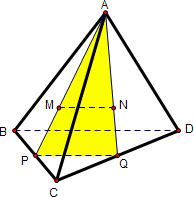 解:∵BC=5,CD=8,∠BCD=60°
解:∵BC=5,CD=8,∠BCD=60°
由余弦定理得:BD=7
延长AM交BC于P,延长AN交CD于Q,
则∵M、N分别是△ABC和△ACD的重心
∴PQ分别BC,CD的中点,
则PQ为△BCD的中位线
∴PQ∥BD且PQ=
=
∵AM:AP=AN:AQ=2:3
∴MN=
PQ=
故答案为:
 解:∵BC=5,CD=8,∠BCD=60°
解:∵BC=5,CD=8,∠BCD=60°由余弦定理得:BD=7
延长AM交BC于P,延长AN交CD于Q,
则∵M、N分别是△ABC和△ACD的重心
∴PQ分别BC,CD的中点,
则PQ为△BCD的中位线
∴PQ∥BD且PQ=
| BD |
| 2 |
| 7 |
| 2 |
∵AM:AP=AN:AQ=2:3
∴MN=
| 2 |
| 3 |
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:当我们已知三角形三边之长求三个角,或是已知三角形两边长及一个夹角求另一边时,常使用余弦定理处理.

练习册系列答案
相关题目
 A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心,若BD=4,试求MN的长.
A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心,若BD=4,试求MN的长.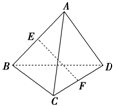 如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.