题目内容
(本小题满分12分)
已知定直线l:x=1和定点M(t,0)(t∈R),动点P到M的距离等于点P到直线l距离的2倍。
(1)求动点P的轨迹方程,并讨论它表示什么曲线;
(2)当t=4时,设点P的轨迹为曲线C,过点M作倾斜角为θ(θ>0)的直线交曲线C于A、B两点,直线l与x轴交于点N。若点N恰好落在以线段AB为直径的圆上,求θ的值。
【答案】
解:(1)设P(x,y),则由题意得=2|x-1|,化简得3x2-y2+2(t-4)x+4-t2=0
 ,………………………4分;
,………………………4分;
当t=1时,化简得 y=±(x-1),表示两条直线;
当t≠1时,表示焦点在x轴上的双曲线。……………………6分;
(2)当t=4时,C: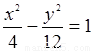 ,M(4,0),N(1,0).由题意知 NA⊥NB,
,M(4,0),N(1,0).由题意知 NA⊥NB,
所以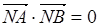 ,
……………………8分;
,
……………………8分;
设A(x1,y1),B(x2,y2),则当AB与x轴垂直时,易得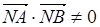 ,不合题意;
,不合题意;
当AB与x轴不垂直时,设AB:y=k(x-4),代入双曲线方程并整理得:
(3-k2)x2+8k2x-16k2-12=0,
由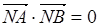 得(x1-1)(x2-2)+y1y2=0
得(x1-1)(x2-2)+y1y2=0
所以 (k2+1)x1x2-(4k2+1)(x1+x2)+16k2+1=0,化简整理得 k2=,所以k=±,……11分
经检验,均符合题意。
所以 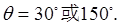 ……………………………12分
……………………………12分
【解析】略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目