题目内容
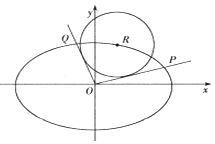
【题目】已知椭圆![]() ,点P(2,0).
,点P(2,0).
(I)求椭圆C的短轴长与离心率;
( II)过(1,0)的直线![]() 与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
【答案】(Ⅰ)短轴长为![]() ,离心率为
,离心率为![]() .(Ⅱ)见解析
.(Ⅱ)见解析
【解析】分析:(Ⅰ)由题意可得![]() ,
,![]() ,于是可得短轴长与离心率.(Ⅱ)方法一:通过判断点P与以MN为直径的圆的位置关系可得结论.方法二:运用作差比较的方法判断大小关系.
,于是可得短轴长与离心率.(Ⅱ)方法一:通过判断点P与以MN为直径的圆的位置关系可得结论.方法二:运用作差比较的方法判断大小关系.
详解:(I)由题意的椭圆的方程为![]() ,
,
∴![]()
∴![]() ,
,![]() .
.
∴椭圆C的短轴长为![]() ,离心率为
,离心率为![]() .
.
(II)方法1:结论是:![]() .
.
当直线![]() 斜率不存在时,
斜率不存在时,![]() .
.
当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]()
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与椭圆交于两点,
与椭圆交于两点,
∴![]() .
.
设![]() ,
,
则![]() .
.
又![]()
![]()
![]()
![]()
![]()
∴![]() ,
,
∴点P在以MN为直径的圆内,
故![]() .
.
(II)方法2:结论是![]() .
.
当直线![]() 斜率不存在时,
斜率不存在时,![]()
当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]()
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与椭圆交于两点,
与椭圆交于两点,
∴![]() .
.
设![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]()
![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目