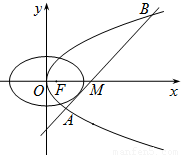
题目内容
已知抛物线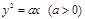 ,直线l与抛物线交于A、B,且
,直线l与抛物线交于A、B,且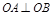 ,点
,点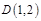 在AB上,又
在AB上,又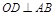 .
.
(1)求直线l的方程;
(2)求a的值;
(3)求△OAB的面积.
【答案】
(1) 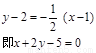 (2)
a=5(3)
(2)
a=5(3)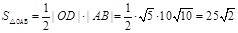
【解析】(1)因为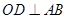 ,所以可根据OD的斜率求出AB的斜率,又因为AB过D点,所以可写出AB的点斜式方程,再化成一般式即可。
,所以可根据OD的斜率求出AB的斜率,又因为AB过D点,所以可写出AB的点斜式方程,再化成一般式即可。
(2)在(1)的基础上,直线l的方程与抛物线方程联立,消去x后得到关于y的一元二次方程,然后根据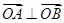 ,借助韦达定理建立关于a的方程求出a的值。
,借助韦达定理建立关于a的方程求出a的值。
(3)利用弦长公式求出底|AB|的长,然后可求出高|OD|的长度,再借助面积公式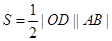 即可求值。
即可求值。
(1) 因为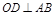 ,
, 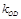 =2,所以
=2,所以 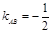 直线l为:
直线l为: 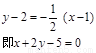 …………3分
…………3分
(2)由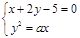 得,
得,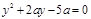 ………………5分
………………5分
设A(x1,y1)、B(x2,y2)则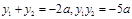 ……………………6分
……………………6分
由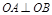 得
得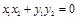 …………………………7分
…………………………7分
又 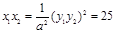 所以:
所以: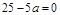 即a=5………………8分
即a=5………………8分
(3)由(2)知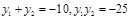 ……………………9分
……………………9分
所以 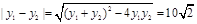
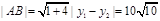 ……10分
……10分
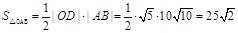

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
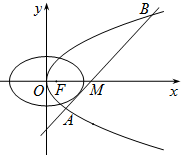 已知抛物线C1的焦点与椭圆C2:
已知抛物线C1的焦点与椭圆C2: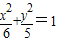 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.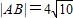 ,求直线l的方程.
,求直线l的方程.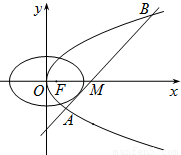
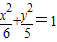 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.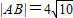 ,求直线l的方程.
,求直线l的方程.