题目内容
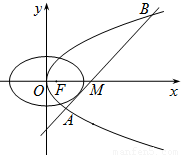
已知抛物线C1的焦点与椭圆C2: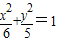 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.(Ⅰ)写出抛物线C1的标准方程;
(Ⅱ)若
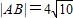 ,求直线l的方程.
,求直线l的方程.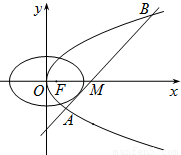
【答案】分析:(1)由抛物线C1的焦点与椭圆C2: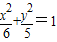 的右焦点重合,知抛物线C1的焦点坐标为F(1,0),再由抛物线C1的顶点在坐标原点,能求出抛物线C1的方程.
的右焦点重合,知抛物线C1的焦点坐标为F(1,0),再由抛物线C1的顶点在坐标原点,能求出抛物线C1的方程.
(2)设直线AB的方程为:y=k(x-4)(k≠0).联立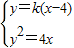 ,得 ky2-4y-16k=0,故△=16+64k2>0,设A(x1,y1),B(x2,y2),则
,得 ky2-4y-16k=0,故△=16+64k2>0,设A(x1,y1),B(x2,y2),则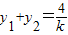 ,y1•y2=-16,利用弦长公式能求出直线l的方程.
,y1•y2=-16,利用弦长公式能求出直线l的方程.
解答:(本小题满分12分)
解:(1)∵抛物线C1的焦点与椭圆C2: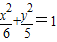 的右焦点重合,
的右焦点重合,
∴抛物线C1的焦点坐标为F(1,0),
∵抛物线C1的顶点在坐标原点,
∴抛物线C1的方程为:y2=4x.…(6分)
(2)若直线AB的斜率不存在时,|AB|=8,不合题意,故直线AB的斜率存在.
由题意可设直线AB的方程为:y=k(x-4)(k≠0).
联立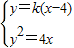 ,消去x,得 ky2-4y-16k=0,
,消去x,得 ky2-4y-16k=0,

∴△=16+64k2>0,设A(x1,y1),B(x2,y2),
则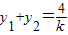 ,y1•y2=-16,
,y1•y2=-16,
∴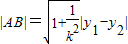
=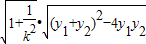
=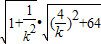
由 ,得k2=1,
,得k2=1,
∴k=±1,
∴直线l的方程为:x-y-4=0或x+y-4=0.…(14分)
点评:本题考查抛物线方程和直线方程的求法,解题时要认真审题,仔细解答,注意抛物线的简单性质、直线与抛物线的位置关系等基本问题的合理运用.
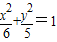 的右焦点重合,知抛物线C1的焦点坐标为F(1,0),再由抛物线C1的顶点在坐标原点,能求出抛物线C1的方程.
的右焦点重合,知抛物线C1的焦点坐标为F(1,0),再由抛物线C1的顶点在坐标原点,能求出抛物线C1的方程.(2)设直线AB的方程为:y=k(x-4)(k≠0).联立
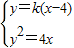 ,得 ky2-4y-16k=0,故△=16+64k2>0,设A(x1,y1),B(x2,y2),则
,得 ky2-4y-16k=0,故△=16+64k2>0,设A(x1,y1),B(x2,y2),则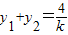 ,y1•y2=-16,利用弦长公式能求出直线l的方程.
,y1•y2=-16,利用弦长公式能求出直线l的方程.解答:(本小题满分12分)
解:(1)∵抛物线C1的焦点与椭圆C2:
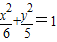 的右焦点重合,
的右焦点重合,∴抛物线C1的焦点坐标为F(1,0),
∵抛物线C1的顶点在坐标原点,
∴抛物线C1的方程为:y2=4x.…(6分)
(2)若直线AB的斜率不存在时,|AB|=8,不合题意,故直线AB的斜率存在.
由题意可设直线AB的方程为:y=k(x-4)(k≠0).
联立
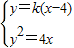 ,消去x,得 ky2-4y-16k=0,
,消去x,得 ky2-4y-16k=0,
∴△=16+64k2>0,设A(x1,y1),B(x2,y2),
则
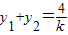 ,y1•y2=-16,
,y1•y2=-16,∴
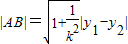
=
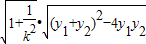
=
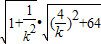
由
 ,得k2=1,
,得k2=1,∴k=±1,
∴直线l的方程为:x-y-4=0或x+y-4=0.…(14分)
点评:本题考查抛物线方程和直线方程的求法,解题时要认真审题,仔细解答,注意抛物线的简单性质、直线与抛物线的位置关系等基本问题的合理运用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
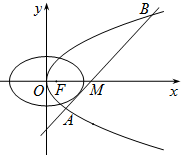 已知抛物线C1的焦点与椭圆C2:
已知抛物线C1的焦点与椭圆C2: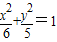 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.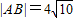 ,求直线l的方程.
,求直线l的方程.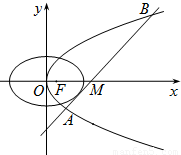
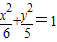 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.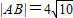 ,求直线l的方程.
,求直线l的方程.