题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在美国广为流传的一道数学题目是:老板给你两种加工资的方案.第一种方案是每年年末(12月底)加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加1000元;第二种方案是每半年(6月底和12月底)各加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加300元,请选择一种.
根据上述条件,试问:
(1)如果你将在该公司干十年,你将选择哪一种加工资的方案?(说明理由)
(2)如果第二种方案中的每半年加300元改成每半年加a元,那么a在什么范围内取值时,选择第二种方案总是比选择第一种方案多加薪?
解:(1)第10年末,依第一方案得
1000+2000+…+10000=55000(元)……………………………………2分
依第二方案得300+300×2+300×3+…+300×20=63000(元)………………4分
∵63000-55000=8000(元)
∴在该公司干10年,选择第二方案比选择第一方案多加薪8000元.………………6分
(2)第n年末,依第一方案,得:1000(1+2+3+…+n)=500n(n+1)(元)……8分
依第二方案,得:a(1+2+3+…+2n)=an(2n+1)……………………………………10分
由题意an(2n+1)>500n(n+1)对所有正整数恒成立………………………………12分
即a>.
∴当a>时,总是第二方案加薪多.………………………………………………14分

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本) 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;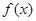 =
=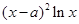 ,
,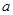 ∈R
∈R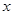 =
=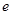 为
为 的极值点,求实数
的极值点,求实数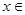 (0,3
(0,3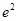 成立.
成立.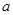 元,每期利率为
元,每期利率为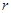 ,设存期为
,设存期为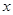 ,本利和(本金加上利息)为
,本利和(本金加上利息)为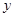 元。
元。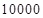 元,每期利率为
元,每期利率为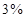 ,试计算
,试计算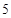 期后的本利和。
期后的本利和。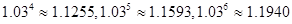 )
) 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,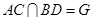 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: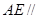 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.