题目内容
若x、y、z均为实数,且a=x2-2y+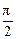 ,b=y2-2z+
,b=y2-2z+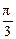 ,c=z2-2x+
,c=z2-2x+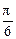 ,则a、b、c中是否至少有一个大于零?请说明理由.
,则a、b、c中是否至少有一个大于零?请说明理由.
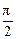 ,b=y2-2z+
,b=y2-2z+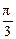 ,c=z2-2x+
,c=z2-2x+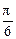 ,则a、b、c中是否至少有一个大于零?请说明理由.
,则a、b、c中是否至少有一个大于零?请说明理由.是
分析:“a、b、c中是否至少有一个大于零”包括多种情况,正面解决很复杂,可考虑反面入手,利用反证法证明,但如何导出矛盾颇有技巧.
假设a、b、c都不大于0,即a≤0,b≤0,c≤0,则a+b+c≤0.
而a+b+c=x2-2y+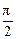 +y2-2z+
+y2-2z+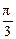 +z2-2x+
+z2-2x+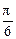 =(x-1)2+(y-1)2+(z-1)2+π-3,
=(x-1)2+(y-1)2+(z-1)2+π-3,
∵π-3>0,且无论x、y、z为何实数,
(x-1)2+(y-1)2+(z-1)2≥0,
∴a+b+c>0.这与a+b+c≤0矛盾.因此,a、b、c中至少有一个大于0.
假设a、b、c都不大于0,即a≤0,b≤0,c≤0,则a+b+c≤0.
而a+b+c=x2-2y+
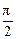 +y2-2z+
+y2-2z+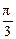 +z2-2x+
+z2-2x+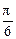 =(x-1)2+(y-1)2+(z-1)2+π-3,
=(x-1)2+(y-1)2+(z-1)2+π-3,∵π-3>0,且无论x、y、z为何实数,
(x-1)2+(y-1)2+(z-1)2≥0,
∴a+b+c>0.这与a+b+c≤0矛盾.因此,a、b、c中至少有一个大于0.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
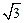 是无理数,q:
是无理数,q: 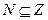 ,q:
,q: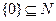
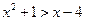 , q:
, q: 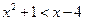
 ,则
,则
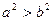 ,则
,则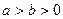
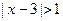 ,则
,则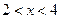
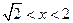 ,则
,则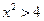
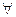 x≥0,x2>0;
x≥0,x2>0;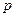 若
若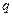 ”的形式,并判断其真假吗?
”的形式,并判断其真假吗? ,则
,则 ”的否命题是 ( )
”的否命题是 ( )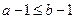
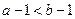
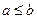 ,则
,则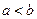 ,则
,则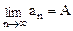 ,
,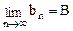 ,则
,则 (
( )
)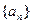 ,
,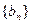 的极限都不存在,则
的极限都不存在,则 的极限也不存在
的极限也不存在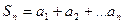 ,若数列
,若数列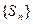 的极限也存在
的极限也存在