题目内容
已知椭圆与双曲线有共同的焦点,F1(0,4),F2(0,4),并且椭圆的长轴点是双曲线实轴长的2倍,求椭圆与双曲线交点的轨迹方程。
解法一:设椭圆与双曲线的交点为P ![]() ,由椭圆、双曲线定义,及已知条件得:
,由椭圆、双曲线定义,及已知条件得:
|
|
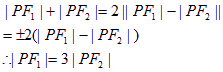
或 ![]()
即 ![]()
化简得 ![]()
或 ![]()
即:![]()
化简得:![]()
∴ 所求轨迹方程为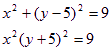
![]()
轨迹是两个圆除去与y轴的交点。
解法二:由题意设双曲线的实半轴长为a ![]()
则椭圆的半长就是a
又∵ c = 4
![]() 为椭圆半短轴
为椭圆半短轴
![]() 为双曲线的虚轴
为双曲线的虚轴
则椭圆方程为![]() ……(1)
……(1)
双曲线方程为![]() ……(2)
……(2)
由(1)×4-(2)得
![]()
即 ![]() ……(3)
……(3)
(3)代入(2)得:
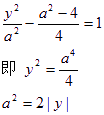
代回(2)中消去a得 ![]()
若![]()
![]()
即 ![]()
即 ![]()
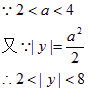
则所求的轨迹是两个圆除去它们与y轴的交点,方程是:
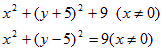
解析:
通过椭圆和双曲线定义,建立动点满足的几何条件,再坐标化而得到轨迹方程。
或由焦点已知曲线中收为原点,坐标轴为对称轴,再需一个条件用待定系法也可求轨迹方程。解法一是将“a”当作参数引进后来后建立方程,不如解法一直接使用定义寻找到动点满足的几何关系简单。

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案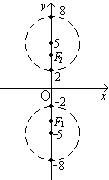
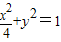 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为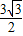 ;
;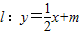 与椭圆有两个交点,求m的取值范围.
与椭圆有两个交点,求m的取值范围. ,且与椭圆
,且与椭圆 有共同的焦点.
有共同的焦点.