题目内容
下列有关命题的说法正确的是 ( )
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则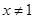 ”. ”. |
B.“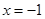 ”是“ ”是“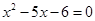 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“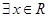 ,使得 ,使得 ”的否定是:“对 ”的否定是:“对 均有 均有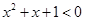 ”. ”. |
D.命题“若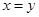 ,则 ,则 ”的逆否命题为真命题. ”的逆否命题为真命题. |
D
解析试题分析:否命题既要否定结论也要否定条件,故A错;由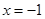 ,能得出
,能得出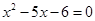 ,但当
,但当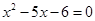 ,
,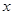 即可以为-1,也可以为6,所以“
即可以为-1,也可以为6,所以“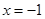 ”是“
”是“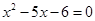 ”的充分不必要条件,B错;命题的否定只否定结论,故C错;因为“若
”的充分不必要条件,B错;命题的否定只否定结论,故C错;因为“若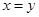 ,则
,则 ”为真命题,故其逆否命题也是真命题,D正确,选D.
”为真命题,故其逆否命题也是真命题,D正确,选D.
考点:命题及其关系.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
“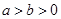 ”是“
”是“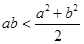 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知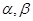 的终边在第一象限,则“
的终边在第一象限,则“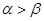 ”是“
”是“ ”( )
”( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若命题“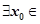 R,使得x02+mx0+2m-3<0”为假命题,则实数m的取值范围是( )
R,使得x02+mx0+2m-3<0”为假命题,则实数m的取值范围是( )
| A.[2,6] | B.[-6,-2] | C.(2,6) | D.(-6,-2) |
下列说法错误的是( )
A.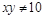 是 是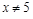 或 或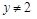 的充分不必要条件 的充分不必要条件 |
B.若命题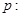 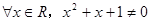 ,则 ,则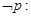 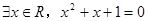 |
C.线性相关系数 的绝对值越接近 的绝对值越接近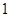 ,表示两变量的相关性越强. ,表示两变量的相关性越强. |
| D.用频率分布直方图估计平均数,可以用每个小矩形的高乘以底边中点横坐标之和. |
“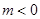 ”是“函数
”是“函数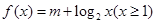 存在零点”的( )
存在零点”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
给出如下四个命题:
①若“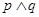 ”为假命题,则
”为假命题,则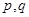 均为假命题;
均为假命题;
②命题“若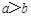 ,则
,则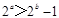 ”的否命题为“若
”的否命题为“若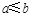 ,则
,则 ”;
”;
③命题“任意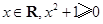 ”的否定是“存在
”的否定是“存在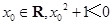 ”;
”;
④在 中,“
中,“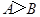 ”是“
”是“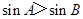 ”的充要条件.
”的充要条件.
其中不正确命题的个数是 ( )
| A.4 | B.3 | C.2 | D.1 |
两个非零向量的模相等是这两个向量相等的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题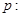
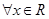 ,
,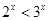 ;命题
;命题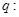
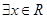 ,
, ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A.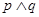 | B.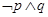 | C.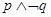 | D.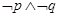 |