题目内容
对于定义域为G的函数f(x),如果同时满足下列两个条件:①f(x)在G内是单调函数;②存在区间[a,b]⊆G,使f(x)在[a,b]上的值域亦为[a,b],那么就称f(x)为好函数.
(Ⅰ)判断函数f(x)=
+1在(0,+∞)上是否为好函数?并说明理由;
(Ⅱ)求好函数f(x)=-x3+1符合条件的一个区间[a,b];
(Ⅲ)若函数f(x)=m+
是好函数,求实数m的取值范围.
(Ⅰ)判断函数f(x)=
| lnx |
| ex |
(Ⅱ)求好函数f(x)=-x3+1符合条件的一个区间[a,b];
(Ⅲ)若函数f(x)=m+
| x+2 |
分析:(I)求出函数的导函数,由f′(e)<0,f′(1)>0,可得f(x)=
+1在(0,+∞)上不是单调函数,再由好函数的定义,可得结论
(Ⅱ)由f(x)=-x3+1在[a,b]上减函数,可得f(a)=b,f(b)=a,即
且a<b,解方程组求出a,b值可得符合条件的区间[a,b];
(III)利用导数法可得f(x)=m+
在[-2,+∞)上为增函数,若函数f(x)=m+
是好函数,则
,即a,b是方程x=m+
的两个相异实根,即
两个相异实根,令f(x)=x2-(2m+1)x+m2-2,分m≤-2时,和m>-2时两种情况讨论m的取值范围,最后综合讨论结果可得答案.
| lnx |
| ex |
(Ⅱ)由f(x)=-x3+1在[a,b]上减函数,可得f(a)=b,f(b)=a,即
|
(III)利用导数法可得f(x)=m+
| x+2 |
| x+2 |
|
| x+2 |
|
解答:解:(Ⅰ)∵函数f(x)=
+1
∴f′(x)=
=
…(1分)
又∵f′(e)<0,f′(1)>0,
∴f(x)=
+1在(0,+∞)上不是单调函数…(1分)
∴f(x)=
+1在(0,+∞)上不是好函数 …(1分)
(Ⅱ)∵f(x)=-x3+1在[a,b]上减函数
∴f(x)的最大值为f(a),最小值为f(b)
故函数f(x)的值域为[f(b),f(a)]…(1分)
∴f(a)=b,f(b)=a
即
且a<b …(1分)
∴解得a=0,b=1,故符合条件的一个闭区间为[0,1]…(1分)
(Ⅲ)∵f(x)=m+
是好函数,
∴存在区间[a,b]⊆[-2,+∞),使f(x)=m+
在[a,b]上的值域亦为[a,b]…(1分)
∵f′(x)=
>0恒成立
故f(x)=m+
在[-2,+∞)上为增函数
∴
∴a,b是方程x=m+
的两个相异实根,且a<b
由x=m+
得:x2-(2m+1)x+m2-2=0
故
两个相异实根
令f(x)=x2-(2m+1)x+m2-2
(ⅰ)当m≤-2时,可得
解得:m>-
∴-
<m≤-2 …(2分)
(ⅱ)当m>-2时,
解得-
<m≤-2,不符合题意
故综上,m的取值范围为-
<m≤-2 …(2分)
【注】:对(Ⅲ),若不讨论但答案对,则扣(2分).
| lnx |
| ex |
∴f′(x)=
| ||
| e2x |
ex•(
| ||
| e2x |
又∵f′(e)<0,f′(1)>0,
∴f(x)=
| lnx |
| ex |
∴f(x)=
| lnx |
| ex |
(Ⅱ)∵f(x)=-x3+1在[a,b]上减函数
∴f(x)的最大值为f(a),最小值为f(b)
故函数f(x)的值域为[f(b),f(a)]…(1分)
∴f(a)=b,f(b)=a
即
|
∴解得a=0,b=1,故符合条件的一个闭区间为[0,1]…(1分)
(Ⅲ)∵f(x)=m+
| x+2 |
∴存在区间[a,b]⊆[-2,+∞),使f(x)=m+
| x+2 |
∵f′(x)=
| 1 | ||
2
|
故f(x)=m+
| x+2 |
∴
|
∴a,b是方程x=m+
| x+2 |
由x=m+
| x+2 |
故
|
令f(x)=x2-(2m+1)x+m2-2
(ⅰ)当m≤-2时,可得
|
解得:m>-
| 9 |
| 4 |
∴-
| 9 |
| 4 |
(ⅱ)当m>-2时,
|
解得-
| 9 |
| 4 |
故综上,m的取值范围为-
| 9 |
| 4 |
【注】:对(Ⅲ),若不讨论但答案对,则扣(2分).
点评:本题考查的知识点是函数单调性的判断与证明,函数与方程的综合应用,正确理解“好函数”的定义,并能根据定义,归纳整理解答相关问题的方法和步骤是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
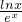 +1在(0,+∞)上是否为好函数?并说明理由;
+1在(0,+∞)上是否为好函数?并说明理由;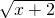 是好函数,求实数m的取值范围.
是好函数,求实数m的取值范围.