题目内容
(2013•浙江)设a,b∈R,定义运算“∧”和“∨”如下:
a∧b= a∨b=
a∨b=
若正数a、b、c、d满足ab≥4,c+d≤4,则( )
a∧b=
 a∨b=
a∨b=
若正数a、b、c、d满足ab≥4,c+d≤4,则( )
| A.a∧b≥2,c∧d≤2 | B.a∧b≥2,c∨d≥2 | C.a∨b≥2,c∧d≤2 | D.a∨b≥2,c∨d≥2 |
C
∵a∧b= ,a∨b=
,a∨b= ,
,
正数a、b、c、d满足ab≥4,c+d≤4,
∴不妨令a=1,b=4,则a∧b≥2错误,故可排除A,B;
再令c=1,d=1,满足条件c+d≤4,但不满足c∨d≥2,故可排除D;
故选C.
 ,a∨b=
,a∨b= ,
,正数a、b、c、d满足ab≥4,c+d≤4,
∴不妨令a=1,b=4,则a∧b≥2错误,故可排除A,B;
再令c=1,d=1,满足条件c+d≤4,但不满足c∨d≥2,故可排除D;
故选C.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
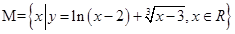 ,
,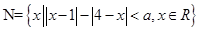
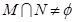 ,则实的数
,则实的数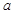 取值范围是____________ .
取值范围是____________ . 有且仅有2个子集,则满足条件的实数
有且仅有2个子集,则满足条件的实数 的个数是 .
的个数是 .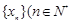 ,数列
,数列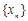 至少有两项)且
至少有两项)且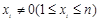 ,定义集合
,定义集合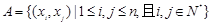 .若对任意点
.若对任意点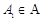 ,
,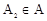 使得
使得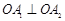
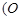 为坐标原点),则称数列
为坐标原点),则称数列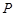 .
.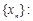 -2,2具有性质
-2,2具有性质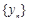 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质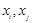 ,使得
,使得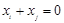 ;
;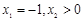 且
且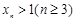 ,则
,则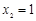 .
.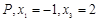 ,则
,则 .
.