题目内容
已知(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() 为
为![]() 在区间
在区间![]() 上的最小值。
上的最小值。
(i)写出![]() 的表达式;
的表达式;
(ii)求![]() 的取值范围,使得
的取值范围,使得![]() 。
。
本题主要考查函数的性质、求导、导数的应用等基础知识,同时考查分类讨论思想以及综合运用所学知识分析问题和解决问题的能力.
(Ⅰ)解:函数的定义域为![]() ,
,
![]() (
(![]() ).
).
若![]() ,则
,则![]() ,
,
![]() 有单调递增区间
有单调递增区间![]() .
.
若![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
![]() 有单调递减区间
有单调递减区间![]() ,单调递增区间
,单调递增区间![]() .
.
(Ⅱ)解:(i)若![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() .
.
若![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .
.
若![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
综上所述,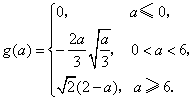
(ii)令![]() .
.
若![]() ,无解.
,无解.
若![]() ,解得
,解得![]() .
.
若![]() ,解得
,解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
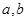 是实数,函数
是实数,函数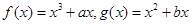 ,
,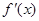 和
和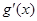 ,分别是
,分别是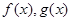 的导函数,若
的导函数,若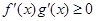 在区间
在区间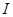 上恒成立,则称
上恒成立,则称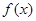 和
和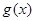 在区间
在区间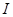 上单调性一致.
上单调性一致.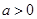 ,若函数
,若函数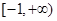 上单调性一致,求实数
上单调性一致,求实数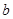 的取值范围;
的取值范围;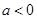 且
且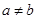 ,若函数
,若函数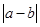 的最大值.
的最大值.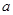 是实数,函数
是实数,函数 。
。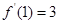 ,求
,求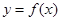 在点
在点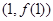 处的切线方程;
处的切线方程;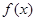 在区间
在区间 上的最大值。
上的最大值。 是实数,函数
是实数,函数 .
.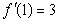 ,求
,求 在点
在点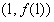 处的切线方程;
处的切线方程;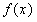 在区间
在区间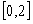 上的最大值.
上的最大值.