题目内容
已知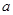 是实数,函数
是实数,函数 。
。
(Ⅰ)若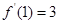 ,求
,求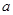 的值及曲线
的值及曲线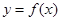 在点
在点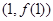 处的切线方程;
处的切线方程;
(Ⅱ)求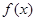 在区间
在区间 上的最大值。
上的最大值。
【答案】
(1)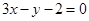 (2)
(2)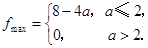
【解析】
试题分析:(Ⅰ)解: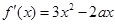 ,
,
因为 ,
,
所以 .
.
又当 时,
时,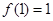 ,
,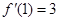 ,
,
所以曲线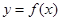 在
在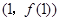 处的切线方程为
处的切线方程为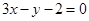 .
.
(Ⅱ)解:令 ,解得
,解得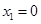 ,
,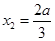 .
.
当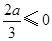 ,即
,即 时,
时,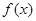 在
在 上单调递增,从而
上单调递增,从而
 .
.
当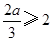 ,即
,即 时,
时,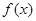 在
在 上单调递减,从而
上单调递减,从而
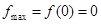 .
.
当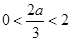 ,即
,即 时,
时,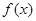 在
在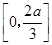 上单调递减,在
上单调递减,在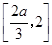 上单调递增,从而
上单调递增,从而
综上所述, 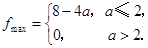
考点:函数的最值
点评:该试题属于常规试题,解题的时候只要审题清晰,表示为数学代数式即可,让那后金额和函数求解最值。属于基础题。

练习册系列答案
相关题目
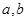 是实数,函数
是实数,函数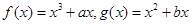 ,
,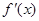 和
和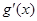 ,分别是
,分别是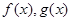 的导函数,若
的导函数,若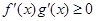 在区间
在区间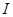 上恒成立,则称
上恒成立,则称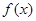 和
和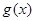 在区间
在区间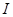 上单调性一致.
上单调性一致.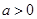 ,若函数
,若函数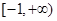 上单调性一致,求实数
上单调性一致,求实数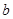 的取值范围;
的取值范围;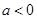 且
且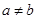 ,若函数
,若函数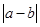 的最大值.
的最大值. 是实数,函数
是实数,函数 .
.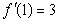 ,求
,求 在点
在点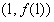 处的切线方程;
处的切线方程;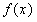 在区间
在区间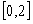 上的最大值.
上的最大值.