题目内容
(07年广东卷) (l4分)已知![]() 是实数,函数
是实数,函数![]() .如果函数
.如果函数![]() 在区间
在区间![]() 上有零点.求
上有零点.求![]() 的取值范围.
的取值范围.
解析1:当a=0时,函数为f (x)=2x -3,其零点x=![]() 不在区间[-1,1]上。
不在区间[-1,1]上。
当a≠0时,函数f (x) 在区间[-1,1]分为两种情况:
①函数在区间[─1,1]上只有一个零点,此时
![]()
或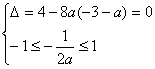
解得1≤a≤5或a=![]()
②函数在区间[─1,1]上有两个零点,此时
 或
或
解得a![]() 5或a<
5或a<![]()
综上所述,如果函数在区间[─1,1]上有零点,那么实数a的取值范围为
(-∞, ![]() ]∪[1, +∞).
]∪[1, +∞).
解析2:a=0时,不符合题意,所以a≠0,又
∴![]() =0在[-1,1]上有解,
=0在[-1,1]上有解,![]() 在[-1,1]上有解
在[-1,1]上有解![]() 在[-1,1]上有解,问题转化为求函数
在[-1,1]上有解,问题转化为求函数![]() [-1,1]上的值域;设t=3-2x,x∈[-1,1],则
[-1,1]上的值域;设t=3-2x,x∈[-1,1],则![]() ,t∈[1,5],
,t∈[1,5],![]() ,
,
设![]() ,
,![]() 时,
时,![]() ,此函数g(t)单调递减,
,此函数g(t)单调递减,![]() 时,
时,![]() >0,此函数g(t)单调递增,∴y的取值范围是
>0,此函数g(t)单调递增,∴y的取值范围是![]() ,∴
,∴![]() =0在[-1,1]上有解ó
=0在[-1,1]上有解ó![]() ∈
∈![]()
![]() 或
或![]() 。
。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

