题目内容
求sin220°+cos280°+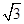 sin20°cos80°的值.
sin20°cos80°的值.
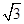 sin20°cos80°的值.
sin20°cos80°的值.
sin220°+cos280°+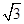 sin20°cos80°=
sin20°cos80°= (1-cos40°)+
(1-cos40°)+
 (1+cos160°)+
(1+cos160°)+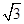 sin20°cos(60°+20°)
sin20°cos(60°+20°)
=1- cos40°+
cos40°+ (cos120°cos40°-sin120°sin40°)+
(cos120°cos40°-sin120°sin40°)+
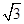 sin20°(cos60°cos20°-sin60°sin20°)
sin20°(cos60°cos20°-sin60°sin20°)
=1- cos40°-
cos40°- cos40°-
cos40°- sin40°+
sin40°+ sin40°-
sin40°-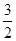 sin220°
sin220°
=1- cos40°-
cos40°- (1-cos40°)=
(1-cos40°)= .
.
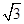 sin20°cos80°=
sin20°cos80°= (1-cos40°)+
(1-cos40°)+ (1+cos160°)+
(1+cos160°)+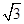 sin20°cos(60°+20°)
sin20°cos(60°+20°)=1-
 cos40°+
cos40°+ (cos120°cos40°-sin120°sin40°)+
(cos120°cos40°-sin120°sin40°)+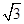 sin20°(cos60°cos20°-sin60°sin20°)
sin20°(cos60°cos20°-sin60°sin20°)=1-
 cos40°-
cos40°- cos40°-
cos40°- sin40°+
sin40°+ sin40°-
sin40°-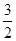 sin220°
sin220°=1-
 cos40°-
cos40°- (1-cos40°)=
(1-cos40°)= .
.
练习册系列答案
相关题目
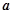
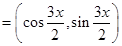 ,
,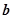
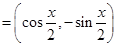 ,且
,且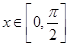
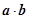 及
及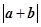
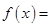
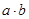 -
-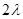
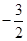 ,求
,求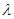 的值。.
的值。.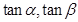 是方程
是方程 的两根,则
的两根,则 .
.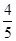 ,cosB=
,cosB=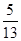 ,则cosC=________.
,则cosC=________. ,tanα=
,tanα= ,求:
,求: 的值.
的值.
 ,若
,若 是实数,且
是实数,且 ,则
,则 的最小值为( )
的最小值为( )


 ,则
,则 是( )
是( )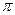 的奇函数
的奇函数 的奇函数
的奇函数 ,
, ,则
,则 的值为 .
的值为 .