题目内容
若方程 +
+ =1所表示的曲线为C,则下面四个命题
=1所表示的曲线为C,则下面四个命题
①若C为椭圆,则1<t<4 ;②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;④若C为椭圆, 且长轴在x轴上,则1<t<
且长轴在x轴上,则1<t<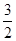
其中真命题的序号是_________.
【答案】
②
【解析】
试题分析:据椭圆方程的特点列出不等式求出t的范围判断出①错,据双曲线方程的特点列出不等式求出t的范围,判断出②对;据圆方程的特点列出方程求出t的值,判断出③错;据椭圆方程的特点列出不等式求出t的范围,判断出④错.解:若C为椭圆应该满足(4-t)(t-1)>0,4-t≠t-1
即1<t<4且t≠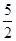 故①错,若C为双曲线应该满足(4-t)(t-1)<0即t>4或t<1故②对,当4-t=t-1即t=
故①错,若C为双曲线应该满足(4-t)(t-1)<0即t>4或t<1故②对,当4-t=t-1即t=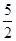 表示圆,故③错,若C表示椭圆,且长轴在x轴上应该满足4-t>t-1>0则1<t<
表示圆,故③错,若C表示椭圆,且长轴在x轴上应该满足4-t>t-1>0则1<t<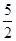 ,因此④错,故填写②
,因此④错,故填写②
考点:圆锥曲线的共同特征。
点评:主要是考查了椭圆方程于双曲线方程的标准形式的运用,属于中档题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 +
+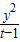 =1所表示的曲线为C,给出下列四个命题:
=1所表示的曲线为C,给出下列四个命题: .
.