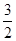题目内容
若方程 +
+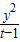 =1所表示的曲线为C,给出下列四个命题:
=1所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<
 .
.其中真命题的序号为33.
A.①②
B.②③
C.③④
D.②④
【答案】分析:利用椭圆、双曲线、圆的标准方程即可得出.
解答:解:①满足4-t>0,t-1>0且4-t≠t-1,即1<t<4且 时表示椭圆,故①不正确;
时表示椭圆,故①不正确;
②满足(4-t)(t-1)<0,解得t>4或t<1时表示双曲线;
③当4-t=t-1>0,即t= 时表示圆,因此③不正确;
时表示圆,因此③不正确;
④当4-t>t-1>0时,即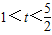 时表示焦点在x轴上的椭圆,因此正确.
时表示焦点在x轴上的椭圆,因此正确.
综上可知:真命题为②④.
故答案为②④.
点评:熟练掌握椭圆、双曲线、圆的标准方程是解题的关键.
解答:解:①满足4-t>0,t-1>0且4-t≠t-1,即1<t<4且
 时表示椭圆,故①不正确;
时表示椭圆,故①不正确;②满足(4-t)(t-1)<0,解得t>4或t<1时表示双曲线;
③当4-t=t-1>0,即t=
 时表示圆,因此③不正确;
时表示圆,因此③不正确;④当4-t>t-1>0时,即
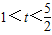 时表示焦点在x轴上的椭圆,因此正确.
时表示焦点在x轴上的椭圆,因此正确.综上可知:真命题为②④.
故答案为②④.
点评:熟练掌握椭圆、双曲线、圆的标准方程是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 +
+ =1所表示的曲线为C,则下面四个命题
=1所表示的曲线为C,则下面四个命题 且长轴在x轴上,则1<t<
且长轴在x轴上,则1<t<